2.用铁管做一个形状为直角三角形的铁框架，要使直角三角形面积为1平方米，有下列四种长度的铁管，最合理(够用，浪费又最少)的是(　　 )

A.4.1米　　　　　　 B.4.8米　　　　 C.5米　　　　 D.5.2米

1.对函数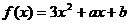作代换x=g(t)，则总不改变f(x)值域的代换是 (　　 )　 A.　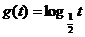 　　　　　　　　　 B.

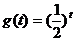
　　 C.g(t)=(t－1)²　　　　　　　　　　　 D.g(t)=cost

1.为了能较快地解决函数综合问题，要求各位学生

⑴在全面复习函数有关知识的基础上，进一步深刻理解函数的有关概念，全面把握各类函数的特征，提高运用基础知识解决问题的能力.

⑵掌握初等数学研究函数的方法，提高研究函数的能力，重视数形结合数学思想方法的运用和推理论证能力的培养.

⑶初步沟通函数与方程、不等式及解析几何有关知识的横向联系，提高综合运用知识解决问题的能力.

⑷树立函数思想，使学生善于用运动变化的观点分析问题.

4.函数应用题主要研究如何利用函数思想解决生产实践中的实际问题，要求各位同学有较宽的知识面，能读懂题意，然后对问题进行分析，灵活运用所学过的数学知识，建立量与量的函数关系，把实际问题材转化为函数问题，通过对函数问题材的解决达到实际问题解决目的.

3.要重视综合运用知识分析问题解决问题的能力和推理论证能力的培养.函数是数学复习的开始，还不可能在大范围内综合运用知识.但从复习开始就让学生树立综合运用知识解决问题的意识是十分重要的.推理论证能力是学生的薄弱环节，近几年高考命题中加强对这方面的考查，尤其是对代数推理论证能力的考查是十分必要的.本课题在例题安排上作了这方面的考虑.

2.以数学知识为载体突出数学思想方法.数学思想方法是观念性的东西，是解决数学问题的灵魂，同时它又离不开具体的数学知识.函数内容最重要的数学思想是函数思想和数形结合的思想.此外还应注意在解题中运用的分类讨论、换元等思想方法.解较综合的数学问题要进行一系列等价转化或非等价转化.因此本课题也十分重视转化的数学思想.

1.在应用中深化基础知识.在复习中基础知识经历一个由分散到系统，由单一到综合的发展过程.这个过程不是一次完成的，而是螺旋式上升的.因此要在应用深化基础知识的同时，使基础知识向深度和广度发展.

8.已知二次函数f(x)=ax²+bx+c.

(1)若a>b>c且f(1)=0，证明：f(x)的图像与X轴相交；

(2)证明：若对x₁、x₂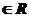，且f(x₁)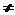f(x₂),则方程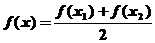必有一实根在区间(x₁,x₂)内；

(3)在(1)的条件下，是否存在实数m，使f(m) = －a成立时,f(m+3)>0.

§2.5　函数的综合运用