
7.某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两个观测点晚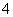
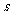 ,已知各观测点到中心的距离都是
,已知各观测点到中心的距离都是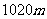 ,试确定该巨响发生的位置.(假定当时声音传播的速度为
,试确定该巨响发生的位置.(假定当时声音传播的速度为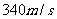 ;相关各点均在同一平面上)
;相关各点均在同一平面上)
6.如图, 7.设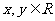
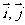 为直角坐标平面内
为直角坐标平面内 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量
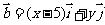 ,
, ,求点
,求点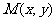 的轨迹C的方程.
的轨迹C的方程.
5.已知椭圆 的两个焦点分别是F1、F2,△MF1F2的重心G恰为椭圆上的点,则点
的两个焦点分别是F1、F2,△MF1F2的重心G恰为椭圆上的点,则点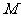 的轨迹方程为
.
的轨迹方程为
.
4.自椭圆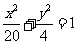 上的任意一点
上的任意一点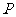 向
向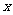 轴引垂线,垂足为
轴引垂线,垂足为 ,则线段
,则线段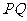 的中点
的中点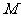 的轨迹方程为
的轨迹方程为
3.已知抛物线 的顶点为
的顶点为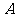 ,那么当
,那么当 变化时,此抛物线焦点
变化时,此抛物线焦点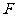 的轨迹方程是___________________________.
的轨迹方程是___________________________.
2.已知椭圆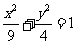 的左、右顶点分别为
的左、右顶点分别为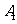 和
和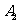 ,垂直于椭圆长轴的动直线与椭圆的两个交点分别为
,垂直于椭圆长轴的动直线与椭圆的两个交点分别为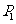 和
和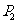 ,其中
,其中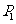 的纵坐标为正数,则直线
的纵坐标为正数,则直线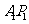 与
与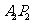 的交点
的交点 的轨迹方程
(
)
的轨迹方程
(
)


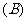
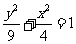

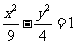


1.抛物线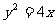 经过焦点的弦的中点的轨迹方程是
( )
经过焦点的弦的中点的轨迹方程是
( )

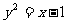
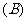
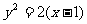

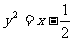


(三)参数法:设动弦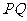 的方程为
的方程为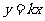 ,由
,由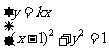 得:
得:
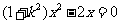 ,设
,设 ,
,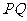 的中点为
的中点为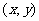 ,则:
,则:
 ,
,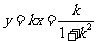 消去
消去 得
得
例2.求过点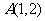 ,离心率为
,离心率为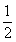 ,且以
,且以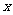 轴为准线的椭圆的下方的顶点轨迹方程.
轴为准线的椭圆的下方的顶点轨迹方程.
解:设椭圆下方的焦点 ,椭圆的下方的顶点为
,椭圆的下方的顶点为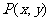
由定义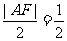 ,∴
,∴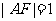 ,即点
,即点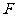 的轨迹方程是
的轨迹方程是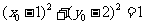 ,
,
又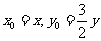 ,∴点的
,∴点的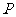 轨迹方程为
轨迹方程为 .
.
例3.设椭圆方程为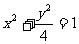 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足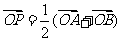 ,点N的坐标为
,点N的坐标为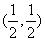 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:
(1)动点P的轨迹方程;
(2)
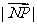 的最小值与最大值.
的最小值与最大值.
(1)解法一:直线l过点M(0,1)设其斜率为k,则l的方程为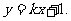
记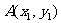 、
、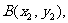 由题设可得点A、B的坐标
由题设可得点A、B的坐标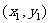 、
、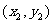 是方程组
是方程组

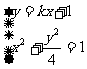 的解.
的解.
将①代入②并化简得,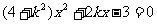 ,所以
,所以
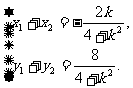 于是
于是
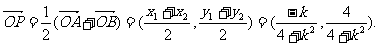
设点P的坐标为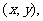 则
则
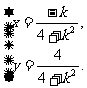 消去参数k得
消去参数k得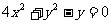 ③
③
当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以点P的轨迹方程为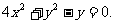
解法二:设点P的坐标为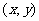 ,因
,因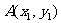 、
、 在椭圆上,所以
在椭圆上,所以
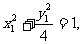 ④
④
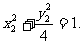 ⑤
⑤
④-⑤得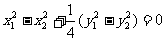 ,所以
,所以
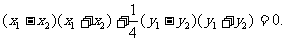
当 时,有
时,有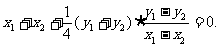 ⑥
⑥
并且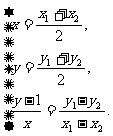 ⑦
⑦
将⑦代入⑥并整理得 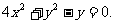 ⑧
⑧
当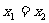 时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为(0,0)
时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为(0,0)
也满足⑧,所以点P的轨迹方程为
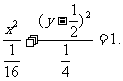
(二)定义法:∵ ,动点
,动点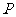 在以
在以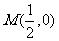 为圆心,
为圆心,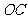 为直径的圆上,
为直径的圆上,
∴所求点的轨迹方程为
例1.动圆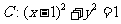 ,过原点
,过原点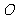 作圆的任一弦,求弦的中点的轨迹方程.
作圆的任一弦,求弦的中点的轨迹方程.
解:(一)直接法:设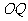 为过
为过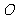 的任一条弦
的任一条弦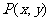 是其中点,则
是其中点,则 ,则
,则 ∴
∴ 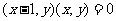 ,即
,即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com