
1.天干地支是我国历史上主要的纪年方式。那么按照该纪年法农历戊戌年后应是:
A.甲子年 B.丁酉年 C.庚子年 D.己亥年
8.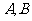 是抛物线
是抛物线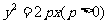 上的两点,且
上的两点,且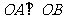 ,
,
(1)求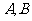 两点的横坐标之积和纵坐标之积;
两点的横坐标之积和纵坐标之积;
(2)求证:直线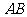 过定点;
过定点;
(3)求弦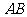 中点
中点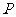 的轨迹方程;
的轨迹方程;
(4)求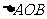 面积的最小值;
面积的最小值;
(5)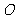 在
在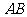 上的射影
上的射影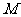 轨迹方程.
轨迹方程.
7.抛物线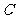 的顶点在坐标原点,对称轴为
的顶点在坐标原点,对称轴为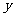 轴,
轴,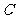 上动点
上动点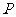 到直线
到直线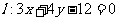 的最短距离为1,求抛物线
的最短距离为1,求抛物线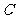 的方程.
的方程.
6.抛物线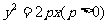 的动弦
的动弦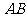 长为
长为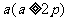 ,则弦
,则弦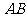 的中点
的中点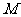 到
到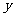 轴的最小距离为
.
轴的最小距离为
.
5.设抛物线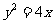 的过焦点的弦的两个端点为A、B,它们的坐标为
的过焦点的弦的两个端点为A、B,它们的坐标为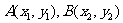 ,若
,若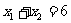 ,那么
,那么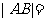 .
.
4.过定点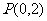 ,作直线
,作直线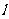 与曲线
与曲线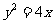 有且仅有1个公共点,则这样的直线
有且仅有1个公共点,则这样的直线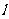 共有 条.
共有 条.
3.抛物线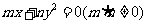 的顶点坐标是 ,焦点坐标是
,准线方程是 ,离心率是 ,通径长
.
的顶点坐标是 ,焦点坐标是
,准线方程是 ,离心率是 ,通径长
.
2.以抛物线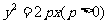 的焦半径
的焦半径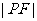 为直径的圆与
为直径的圆与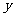 轴位置关系是( )
轴位置关系是( ) 相交
相交  相切
相切  相离
相离  以上三种均有可能
以上三种均有可能
1.方程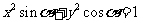 表示的曲线不可能是( )
表示的曲线不可能是( )
 直线
直线
 抛物线
抛物线
 圆
圆
 双曲线
双曲线
例1.抛物线以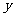 轴为准线,且过点
轴为准线,且过点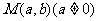 ,证明:不论
,证明:不论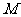 点在坐标平面内的位置如何变化,抛物线顶点的轨迹的离心率是定值.
点在坐标平面内的位置如何变化,抛物线顶点的轨迹的离心率是定值.
例2.已知抛物线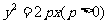 ,过动点
,过动点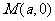 且斜率为
且斜率为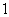 的直线
的直线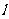 与该抛物线交于不同两点
与该抛物线交于不同两点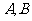 ,
,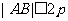 ,
,
(1)求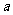 取值范围;(2)若线段
取值范围;(2)若线段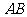 垂直平分线交
垂直平分线交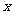 轴于点
轴于点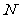 ,求
,求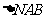 面积的最大值.
面积的最大值.
例3. 已知抛物线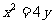 与圆
与圆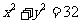 相交于
相交于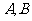 两点,圆与
两点,圆与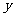 轴正半轴交于
轴正半轴交于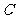 点,直线
点,直线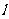 是圆的切线,交抛物线与
是圆的切线,交抛物线与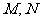 ,并且切点在
,并且切点在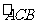 上.
上.
(1)求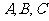 三点的坐标.(2)当
三点的坐标.(2)当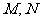 两点到抛物线焦点距离和最大时,求直线
两点到抛物线焦点距离和最大时,求直线 的方程.
的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com