
4.[解析]对A、B、C整体,从C以v0滑上木块到最终B、C达到共同速度V,
其动量守恒既:m v0=2mV1+3mv 1.8=2V1+3×0.4 V1=0.3m/s
对A、B、C整体,从C以v0滑上木块到C以V2刚离开长木板,
此时A、B具有共同的速度V1。其动量守恒即:m v0=mV2+4mv1
3.[解析](1)设第一颗子弹进入靶盒A后,子弹与靶盒的共内速度为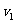 。
。
根据碰撞过程系统动量守恒,有: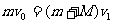
设A离开O点的最大距离为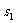 ,由动能定理有:
,由动能定理有: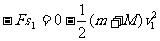
解得: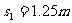
(2)根据题意,A在的恒力F的作用返回O点时第二颗子弹正好打入,由于A的动量与第二颗子弹动量大小相同,方向相反,故第二颗子弹打入后,A将静止在O点。设第三颗子弹打入A后,它们的共同速度为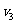 ,由系统动量守恒得:
,由系统动量守恒得: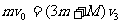 (2分)
(2分)
设A从离开O点到又回到O点所经历的时间为t,取碰后A运动的方向为正方向,由动量定理得: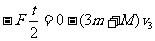 解得:
解得: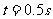
(3)从第(2)问的计算可以看出,第1、3、5、……(2n+1)颗子弹打入A后,A运动时间均为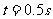 故总时间
故总时间
[答案](1)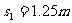 (2)
(2)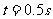 (3)
(3)
2.[解析]①根据图象可知,物体C与物体A相碰前的速度为:v1=6m/s
相碰后的速度为:v2=2m/s 根据定量守恒定律得: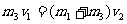 …
…
解得:m3=2.0kg
②规定向左的方向为正方向,在第5.0s和第15s末物块A的速度分别为:
v2=2m/s,v3=-2m/s 所以物块A的动量变化为: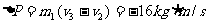
即在5.0s到15s的时间内物块A动量变化的大小为:16kg·m/s 方向向右
[答案](1)m3=2.0kg (2)16kg·m/s 方向向右
1.[解析](1)M静止时,设弹簧压缩量为l0,则Mg=kl0 ①
速度最大时,M、m组成的系统加速度为零,则
(M+m)g-k(l0+l1)=0 ②-
联立①②解得:k=50N/m ③
[或:因M初位置和速度最大时都是平衡状态,故mg=kl1,解得:k=50N/m]
(2)m下落h过程中,mgh=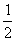 mv02 ④-
mv02 ④-
m冲击M过程中, m v0=(M+m)v ⑤-
所求过程的弹性势能的增加量:ΔE=(M+m)g(l1+l2)+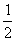 (M+m)v2 ⑥
(M+m)v2 ⑥
联立④⑤⑥解得:ΔE=0.66J ⑦
(用弹性势能公式计算的结果为ΔE=0.65J也算正确)
[答案]ΔE=0.66J
10.[解析]设摆球A、B的质量分别为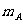 、
、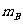 ,摆长为l,B球的初始高度为h1,碰撞前B球的速度为vB.在不考虑摆线质量的情况下,根据题意及机械能守恒定律得
,摆长为l,B球的初始高度为h1,碰撞前B球的速度为vB.在不考虑摆线质量的情况下,根据题意及机械能守恒定律得
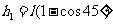 ①
①
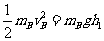 ②
②
设碰撞前、后两摆球的总动量的大小分别为P1、P2。有
P1=mBvB ③
联立①②③式得
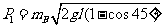 ④
④
同理可得
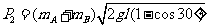 ⑤
⑤
联立④⑤式得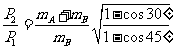
代入已知条件得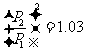 由此可以推出
由此可以推出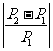 ≤4%
≤4%
所以,此实验在规定的范围内验证了动量守恒定律。
[答案] ≤4%
≤4%
名校试题
9.[解析](1)设B在绳被拉断后瞬间的速度为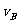 ,到达C点时的速度为
,到达C点时的速度为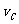 ,有
,有
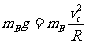 (1)
(1)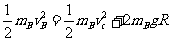 (2)
(2)
代入数据得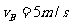 (3)
(3)
(2)设弹簧恢复到自然长度时B的速度为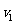 ,取水平向右为正方向,有
,取水平向右为正方向,有
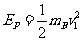 (4)
(4)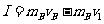 (5)
(5)
代入数据得  其大小为4NS (6)
其大小为4NS (6)
(3)设绳断后A的速度为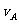 ,取水平向右为正方向,有
,取水平向右为正方向,有
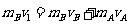 (7)
(7)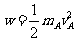 代入数据得
代入数据得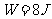
[答案](1)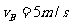 (2)4NS (3)
(2)4NS (3)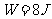
8.[解析]此题开始的绳连的系统,后粘合变成了小球单个质点的运动问题(1)对系统,设小球在最低点时速度大小为v1,此时滑块的速度大小为v2,滑块与挡板接触前由系统的机械能守恒定律:mgl = mv12 +mv22①
由系统的水平方向动量守恒定律:mv1 = mv2②
对滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量为:I = mv2③
联立①②③解得I = m 方向向左④
(2)小球释放到第一次到达最低点的过程中,设绳的拉力对小球做功的大小为W,对小球由动能定理:mgl+W = mv12⑤
联立①②⑤解得:W =-mgl,即绳的拉力对小球做负功,大小为mgl 。
[答案](1)I = m 方向向左;(2)mgl
7.[解析]此题是单个质点碰撞的多过程问题,既可以用动能定理与动量定理求解,也可以用力与运动关系与动量求解.设小物块从高为h处由静止开始沿斜面向下运动,到达斜面底端时速度为v。
由动能定理得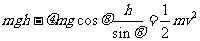 ①
①
以沿斜面向上为动量的正方向。按动量定理,碰撞过程中挡板给小物块的冲量
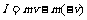 ②
②
设碰撞后小物块所能达到的最大高度为h’,则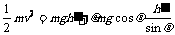 ③
③
同理,有 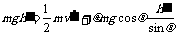 ④
④  ⑤
⑤
式中,v’为小物块再次到达斜面底端时的速度,I’为再次碰撞过程中挡板给小物块的冲量。由①②③④⑤式得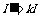 ⑥式中
⑥式中 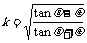 ⑦
⑦
由此可知,小物块前4次与挡板碰撞所获得的冲量成等比级数,首项为
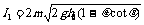 ⑧总冲量为
⑧总冲量为 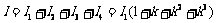 ⑨
⑨
由 (
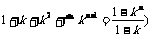 ⑩得
⑩得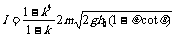 ⑾
⑾
代入数据得 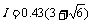 N·s
N·s
[答案] 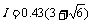 N·s
N·s
6.[解析]⑴碰后B上摆过程机械能守恒,可得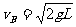 。
。
⑵两球发生弹性碰撞过程系统动量守恒,机械能守恒。设与B碰前瞬间A的速度是v0,有2mv0=2mvA+mvB,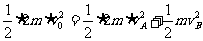 ,可得vA= v0/3,vB= 4v0/3,因此
,可得vA= v0/3,vB= 4v0/3,因此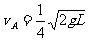 ,同时也得到
,同时也得到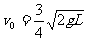 。
。
⑶先由A平抛的初速度vA和水平位移L/2,求得下落高度恰好是L。即两球碰撞点到水平面的高度是L。A离开弹簧时的初动能可以认为就等于弹性力对A做的功。A离开弹簧上升的全过程用机械能守恒: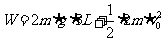 ,解得W=
,解得W= 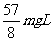
[答案](1)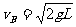 (2)W=
(2)W= 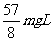
5.[解析]从两小球碰撞后到它们再次相遇,小球A和B的速度大小保持不变。根据它们通过的路程,可知小球B和小球A在碰撞后的速度大小之比为4︰1。
设碰撞后小球A和B 的速度分别为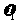 和
和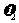 ,在碰撞过程中动量守恒,碰撞前后动能相等,有
,在碰撞过程中动量守恒,碰撞前后动能相等,有
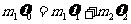 ………… ①
………… ①
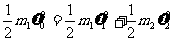 ………… ②
………… ②
联立以上两式再由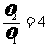 ,可解出 m1∶m2=2∶1
,可解出 m1∶m2=2∶1
[答案]2∶1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com