
5.已知双曲线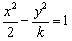 的一条准线与抛物线
的一条准线与抛物线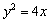 的准线重合,则双曲线的离心率等于( )
的准线重合,则双曲线的离心率等于( )
A.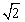 B.
B.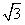 C.2 D.3
C.2 D.3
4.已知命题p:在△ABC中,“A>B”是“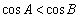 ”成立的充要条件;命题q:“
”成立的充要条件;命题q:“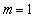 ”是“直线
”是“直线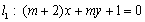 与直线
与直线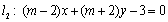 垂直”的充要条件.那么( )
垂直”的充要条件.那么( )
A.“p且q”为真 B.“p或q”为假 C.p假q 真 D.p真q假
3.已知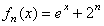 (n
(n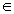
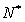 ),则
),则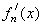 =( )
=( )
A.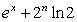 B.
B.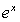 C.
C.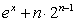 D.
D.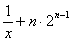
2.定义集合M与N的新运算,M+N={x|x∈M或x∈N且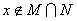 },已知M=Q,N=R,则M+N=(
)
},已知M=Q,N=R,则M+N=(
)
A.{x|x为无理数} B.Q C.R D.Æ
1.已知i是虚数单位,复数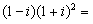 ( )
( )
A.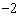 B.
B.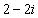 C.
C.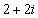 D.2
D.2
22. 解: (1)设M(x,y)是f(x)图象上任一点,则M关于P(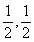 )的对称点为M’(1-x,1-y),
)的对称点为M’(1-x,1-y),
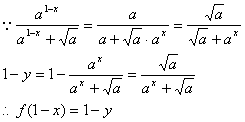
∴M′(1-x,1-y)亦在f(x)的图象上,
故函数f(x)的图象关于点P(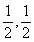 )对称.----------------3分
)对称.----------------3分
(2)将f(n)、f(1-n)的表达式代入an的表达式,化简可得an=an猜a=3,----------6分
即3n>n2.
下面用数学归纳法证明.
设n=k(k≥2)时,3k>k2.
那么n=k+1,3k+1>3·3k>3k2
又3k2-(k+1)2=2(k-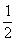 )2-
)2-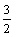 ≥0(k≥2,k∈N)
≥0(k≥2,k∈N)
∴3n>n2.-----------------------------9分
(3)∵3k>k2
∴klg3>2lgk
令k=1,2,…,n,得n个同向不等式,并相加得:
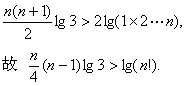 -----------------------12分
-----------------------12分
21. 解:(1)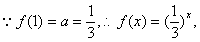
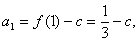
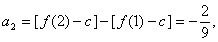
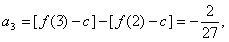
又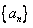 为等比数列,
为等比数列,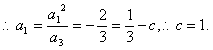 公比
公比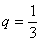
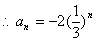 -------4分
-------4分
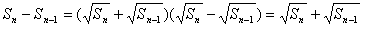 又
又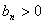
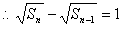 ,数列
,数列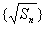 构成一个首项为1公差为1的等差数列,
构成一个首项为1公差为1的等差数列,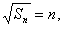
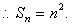
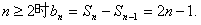 ----------------------------------------------------------8分
----------------------------------------------------------8分
(2)
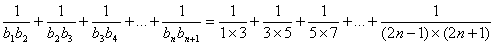
=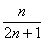 -----------------------------------------------------10分
-----------------------------------------------------10分
由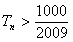 ,得
,得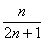
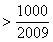 ,
,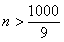 所以
所以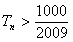 的最小正整数
的最小正整数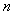 是112.--------12分
是112.--------12分
20.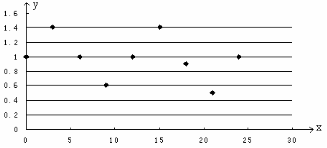 (1)
(1)

(2)由(1)知选择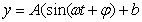 较合适。---------------------------------3分
较合适。---------------------------------3分
由图知,A=0.4,b=1,T=12,
所以,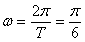 ,把t=0,y=1代入
,把t=0,y=1代入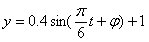 ,
,
得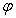 =0,所以,所求的解析式为:
=0,所以,所求的解析式为: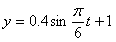 (0≤t≤24)。---------------6分
(0≤t≤24)。---------------6分
(3)由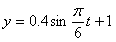 ≥0.8,得
≥0.8,得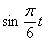 ≥-
≥-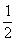 。,
。,
则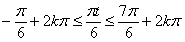 (k
(k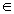 Z),
Z),
即12k-1≤t≤12k+7,
所以,0≤t≤7或11≤t≤19或23≤t≤24
答:应安排在11时到19时训练较恰当。--------------------------------------12分
19.解:(Ⅰ)由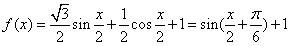 ………………2分
………………2分
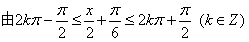
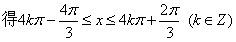
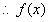 的单调递增区间为
的单调递增区间为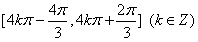 ………………4分
………………4分
(Ⅱ)由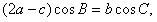
得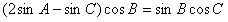 ,
,
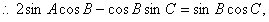
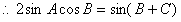
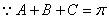 ,
,
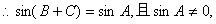
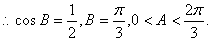
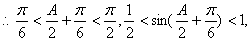
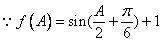 ,
,
 函数
函数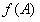 的取值范围是
的取值范围是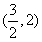 .
………………………12分
.
………………………12分
18.解:(Ⅰ)设等差数列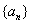 首项为
首项为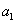 ,公差为
,公差为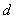 ,由题意,得
,由题意,得
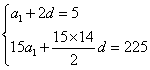 解得
解得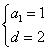
∴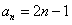 --------------------------4分
--------------------------4分
(Ⅱ)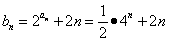 ,----------------6分
,----------------6分
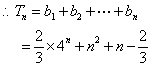 -------------------------------12分
-------------------------------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com