
17. 解:(1)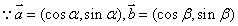 ,
,
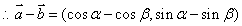 。
。
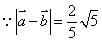 ,
,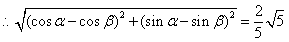 ,
,
即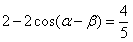 ,
,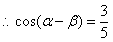 ------------------------5分
------------------------5分
(2)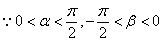 ,
,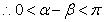 。
。 ,
,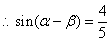 。
。
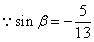 ,
,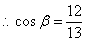 。
。
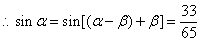 -----------------------------------10分
-----------------------------------10分
13.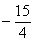 14.
14. 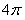 15.
15. 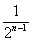 16.
16.
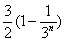
22. (本题12分)已知函数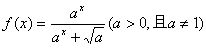 .
.
(1) 证明函数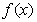 的图象关于点P (
的图象关于点P (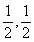 )对称.
)对称.
(2) 令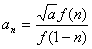 ,对一切自然数
,对一切自然数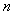 ,先猜想使
,先猜想使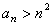 成立的最小自然数
成立的最小自然数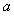 ,并证明之.
,并证明之.
(3) 求证: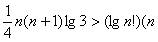 ∈N).
∈N).
高三上学期四调考试(数学理科)
答案:DDBAC BAACD BD.
21. (本题12分) 已知点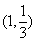 是函数
是函数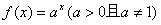 的图象上一点,等比数列
的图象上一点,等比数列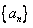 的前
的前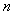 项和为
项和为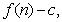 数列
数列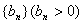 的首项为
的首项为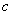 ,且前
,且前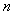 项和
项和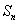 满足
满足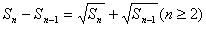
(1)数列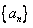 ,
,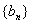 的通项公式;
的通项公式;
(2)若数列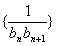 的前
的前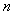 项和为
项和为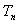 ,问
,问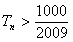 的最小正整数
的最小正整数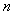 是多少?
是多少?
20. (本题12分)某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度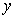 (米)随着时间
(米)随着时间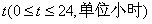 而周期性变化,每天各时刻
而周期性变化,每天各时刻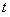 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
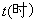 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
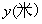 |
1.0 |
1.4 |
1.0 |
0.6 |
1.0 |
1.4 |
0.98 |
0.59 |
1.0 |
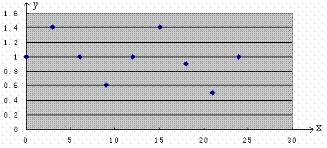
(1)试在图中描出所给点;
(2)观察图,从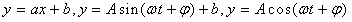 中选择一个合适的函 数模型,并求出该拟合模型的解析式;
中选择一个合适的函 数模型,并求出该拟合模型的解析式;
(3)如果确定在白天7时~19时当浪高不低于0.8米时才进行训练,试安排恰当的训练时间。
19.(本题12分) 已知函数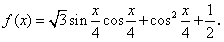
(1)求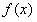 的单调递增区间;
的单调递增区间;
(2)在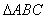 中,角
中,角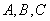 的对边分别是
的对边分别是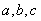 ,且满足
,且满足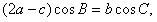 求函数
求函数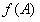 的取值范围.
的取值范围.
18. (本题12分) 已知等差数列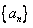 的前
的前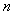 项和为
项和为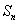 ,且
,且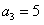 ,
,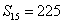 。
。
(1)求数列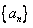 的通项公式;
的通项公式;
(2)设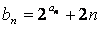 ,求数列
,求数列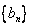 的前
的前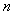 项和
项和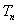 .
.
17. (本题10分) 已知向量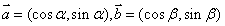 ,
,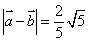 。
。
(1)求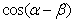 的值;
的值;
(2)若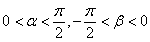 ,且
,且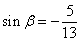 ,求
,求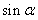 的值。
的值。
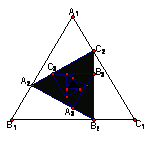
16. 如图,在面积为1的正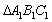 内作正
内作正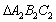 ,使
,使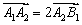 ,
,
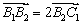 ,
,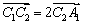 ,依此类推,在正
,依此类推,在正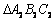 内再作正
内再作正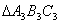 ,……. 记正
,……. 记正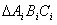 的面积为
的面积为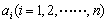 ,则
,则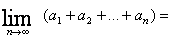 .
.
15. 数列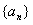 所有项的和为
所有项的和为 ,第二项及以后各项的和为
,第二项及以后各项的和为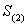 ,第三项及以后各项的和为
,第三项及以后各项的和为 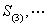 ,第
,第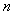 项及以后各项的和为
项及以后各项的和为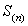 ,若
,若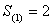 ,
,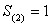 ,
,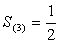 ,…,
,…,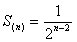 ,
,
则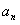 等于 .
等于 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com