
18. [解析](1)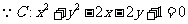
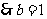 时,点
时,点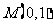 在圆上.又
在圆上.又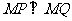
,圆心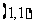 在直线直线
在直线直线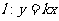 上,故
上,故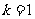 . ………………………..2分
. ………………………..2分
(2)设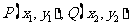 .
.
联立方程组,
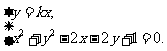
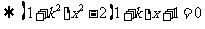 ,
,
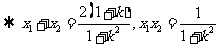 .………………………………………………………. 4分
.………………………………………………………. 4分
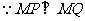
 即
即
又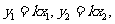
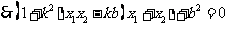 ,………………. 6分
,………………. 6分
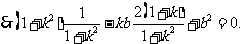
当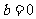 时,此式不成立,
时,此式不成立,
从而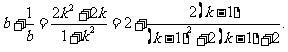 .…………………………. 9分
.…………………………. 9分
又 令
令
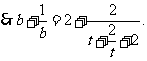 令函数
令函数 当
当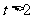 时,
时,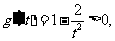
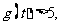 从而
从而 ,……………………………… 11分
,……………………………… 11分
解此不等式,可得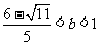 或
或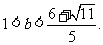 .…………………… 13分
.…………………… 13分
17.[解析]
(I) 共有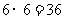 种结果····································································· 4分
种结果····································································· 4分
(II) 若用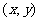 来表示两枚骰子向上的点数所构成的点的坐标,满足
来表示两枚骰子向上的点数所构成的点的坐标,满足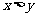 的结果有:
的结果有:
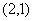 ,(3,1),(4,1)(5,1),(6,1)(3,2),(4,2)(5,2),(6,2)(4,3),
,(3,1),(4,1)(5,1),(6,1)(3,2),(4,2)(5,2),(6,2)(4,3),
(5,3)(6,3),(5,4)(6,4),(6,5)共15种.·································· 8分
(III)满足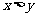 的概率是:P=
的概率是:P=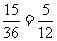 . ··········································· 13分
. ··········································· 13分
16.[解析](Ⅰ)由题意得
 ············································································ 2分
············································································ 2分
因为cosA≠0, ······················································································ 3分
所以tanA=1. ······················································································· 4分
(Ⅱ)由(Ⅰ)知tanA=1得
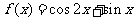 ······································································ 5分
······································································ 5分
= ········································································· 6分
········································································· 6分
=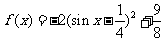 ······························································· 7分
······························································· 7分
因为x R,所以
R,所以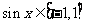 .···································································· 8分
.···································································· 8分
当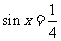 时,f(x)有最大值
时,f(x)有最大值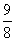 ,···························································· 10分
,···························································· 10分
当sinx=-1时,f(x)有最小值-2,····························································· 11分
所以所求函数f(x)的值域是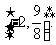 ······················································ 13分
······················································ 13分
(二)选做题(14-15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)[解析]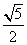 .将极坐标方程
.将极坐标方程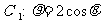 和
和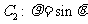 分别化为普通方程
分别化为普通方程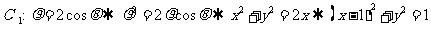 ,
,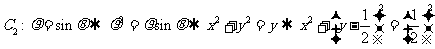 ,然后就可解得答案
,然后就可解得答案 .
.
15.(几何证明选讲选做题)[解析]15.如图,由相交弦定理可知,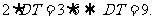
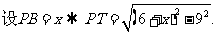
 由切割线定理可知
由切割线定理可知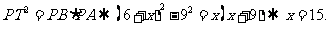
(一)必做题(11-13题)
11.[解析]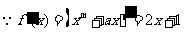 , ,
, ,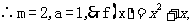 从而数列
从而数列 的前
的前 项和为
项和为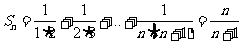 .
.
12.[解析]20.由题意可知
13.[解析] . 由
. 由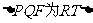 ,又由双曲线
,又由双曲线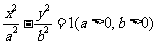 的对称性可知
的对称性可知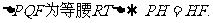 又双曲线的渐近线方程为
又双曲线的渐近线方程为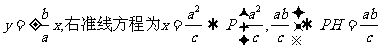 .又因为
.又因为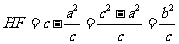 .因为
.因为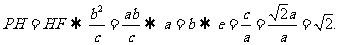
10.[解析]C.由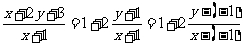 ,考虑到斜率以及由x,y满足约束条件
,考虑到斜率以及由x,y满足约束条件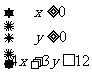 所确定的可行域,数形结合,易得答案为C.
所确定的可行域,数形结合,易得答案为C.
9.[解析]C.由题意“函数f(x)、f(x+2)均为偶函数”可知,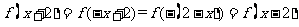
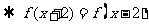
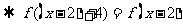
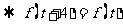
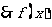 的周期为
的周期为 .从而
.从而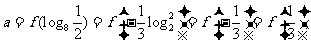
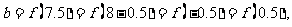
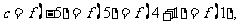
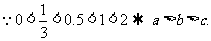 从而选C.
从而选C.
8.[解析]B. 因为函数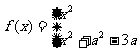
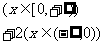 在区间
在区间 是增函数,又因
是增函数,又因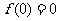 ,所以
,所以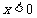 时,
时,


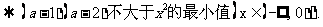
从而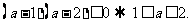 从而选B.
从而选B.
7.[解析]A. 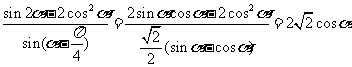 .
.
6.[解析]A.随机取出2个小球得到的结果数有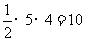 种(提倡列举).取出的小球标注的数字之和为3或6的结果为
种(提倡列举).取出的小球标注的数字之和为3或6的结果为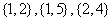 共3种,故所求答案为(A).
共3种,故所求答案为(A).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com