
3. 如果复数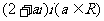 的实部与虚部互为相反数,则
的实部与虚部互为相反数,则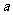 的值等于( )
的值等于( )
A.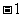 B.
B.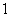 C.
C.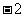 D.
D.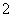
2.已知公差不为0的等差数列 中,有
中,有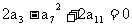 ,数列
,数列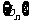 是等比数列,且
是等比数列,且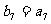 则
则 = ( )
= ( )
 A.2
B.4
C.8
D.16
A.2
B.4
C.8
D.16
1.已知集合P={ 0,m },Q={x│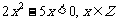 },若P∩Q
≠
},若P∩Q
≠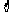 ,则m等于 ( )
,则m等于 ( )
(A) 1 (B) 2
(C) 1或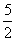 (D)1或2
(D)1或2
22.(本小题满分14分)
已知函数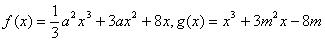 ,
,
(Ⅰ)求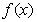 在x=1处的切线斜率的取值范围;
在x=1处的切线斜率的取值范围;
(Ⅱ)求当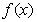 在x=1处的切线的斜率最小时,
在x=1处的切线的斜率最小时,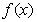 的解析式;
的解析式;
(Ⅲ)在(Ⅱ)的条件下,是否总存在实数m,使得对任意的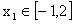 ,总存在
,总存在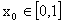 ,使得
,使得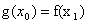 成立?若存在,求出实数m的取值范围;若不存在,说明理由.
成立?若存在,求出实数m的取值范围;若不存在,说明理由.
21. (本小题满分12分)
(本小题满分12分)
某投资公司计划投资A、B两种
金融产品,根据市场调查与预测,A产品
的利润与投资量成正比例,其关系如图1,
 B产品的利润与投资量的算术平方根成正
B产品的利润与投资量的算术平方根成正
比例,其关系如图2,(注:利润与投资量
单位:万元)。
(Ⅰ)分别将A、B两产品的利润表示为投
资量的函数关系式;
(Ⅱ)该公司已有10万元资金,并全部投入
A、B两种产品中,问:怎样分配这10万元投资,
才能使公司获得最大利润?其最大利润为多少万元?
20.(本小题满分12分)
已知函数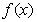 的定义域是
的定义域是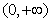 ,当
,当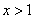 时,
时,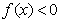 ,且
,且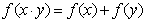 .
.
(Ⅰ)证明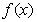 在定义域上是减函数;
在定义域上是减函数;
(Ⅱ)如果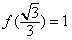 ,求满足不等式
,求满足不等式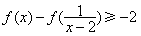 的
的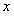 的取值范围.
的取值范围.
19.(本小题满分12分)
已知数列 的各项均为正数,
的各项均为正数,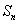 为其前
为其前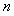 项和,对于任意的
项和,对于任意的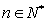 ,满足关系式
,满足关系式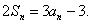
(I)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列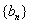 的通项公式是
的通项公式是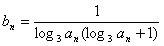 ,前
,前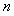 项和为
项和为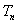 ,求证:对于任意的正整数
,求证:对于任意的正整数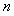 ,总有
,总有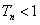
18.(本小题满分12分)
已知经过原点的直线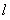 平分抛物线
平分抛物线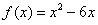 与
与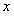 轴所围封闭区域的面积.
轴所围封闭区域的面积.
(I)求抛物线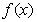 与
与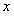 轴所围成封闭区域的面积
轴所围成封闭区域的面积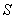 ;
;
(II)求直线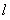 的方程.
的方程.
17.(本小题满分12分)
设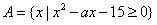 ,
,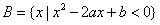 ,
,
A∩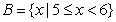 ,求A∪B.
,求A∪B.
16.若函数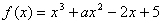 在区间(
在区间(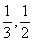 )上既不是单调递增函数,也不是单调递减函数,则实数a的取值范围是__________▲____________.
)上既不是单调递增函数,也不是单调递减函数,则实数a的取值范围是__________▲____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com