8．设0 < a, b, c < 2，求证：(2 - a)c, (2 - b)a, (2 - c)b,不可能同时大于1

仿例四

7．已知a, b, c > 0, 且a² + b² = c²，求证：aⁿ + bⁿ < cⁿ (n≥3, nÎR^*)

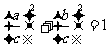　 ∵，又a, b, c > 0, ∴

　 ∴

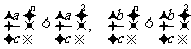
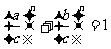
6．

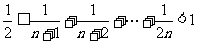
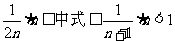
5．

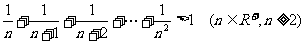
左边

4．若a > b > c,　 则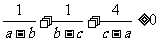

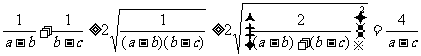
3．　

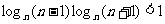
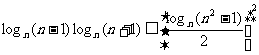
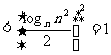
2．　 lg9•lg11 < 1

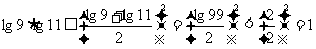
1．　 设x > 0, y > 0,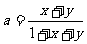, 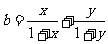，求证：a < b

放缩法：

　 证：设a < 0,　 ∵abc > 0,　 ∴bc < 0

　　　 又由a + b + c > 0,　 则b + c = -a > 0

　　　 ∴ab + bc + ca = a(b + c) + bc < 0　　 与题设矛盾

　　　 又：若a = 0，则与abc > 0矛盾，　 ∴必有a > 0

　　　 同理可证：b > 0,　 c > 0

　 证：设(1 - a)b >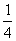,　 (1 - b)c >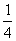,　 (1 - c)a >,

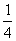则三式相乘：ab < (1 - a)b•(1 - b)c•(1 - c)a <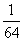　 ①

又∵0 < a, b, c < 1　 ∴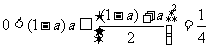

同理：,　

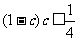
以上三式相乘： (1 - a)a•(1 - b)b•(1 - c)c≤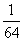　 与①矛盾

∴原式成立