
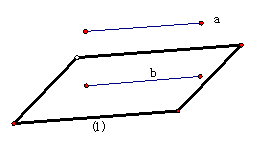
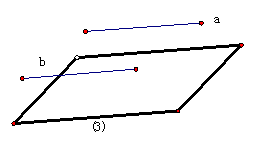
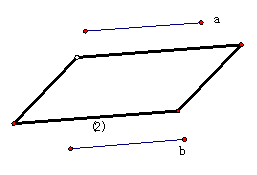
4.C.解析:如图(1),在平面内不可能有符合题意的点;如图(2),直线a、b到已知平面的距离相等且所在平面与已知平面垂直,则已知平面为符合题意的点;如图(3),直线a、b所在平面与已知平面平行,则符合题意的点为一条直线,从而选C.
3.D.解析:由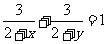 可化为xy
=8+x+y,
可化为xy
=8+x+y, x,y均为正实数,
x,y均为正实数,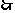 xy =8+x+y
xy =8+x+y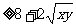 (当且仅当x=y等号成立)即xy-2
(当且仅当x=y等号成立)即xy-2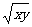 -8
-8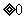 ,可解得
,可解得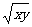
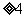 ,即xy
,即xy 16故xy的最小值为16.
16故xy的最小值为16.
解决本题的关键是先变形,再利用基本不等式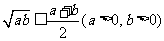 来构造一个新的不等式.
来构造一个新的不等式.
2.C.解析:由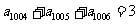 得
得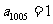 ,从而
,从而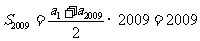 , 选C.若直接用通项公式和求和公式求解较复杂,解答中应用等差数列的性质
, 选C.若直接用通项公式和求和公式求解较复杂,解答中应用等差数列的性质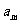 +
+ 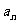 =
=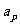 +
+ 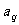 ,结论巧妙产生,过程简捷,运算简单.
,结论巧妙产生,过程简捷,运算简单.
1.B.解析:由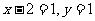 有
有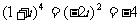 .
.
21.(本小题满分14分)已知数列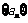 中的各项均为正数,且满足
中的各项均为正数,且满足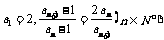 .记
.记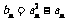 ,数列
,数列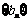 的前
的前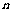 项和为
项和为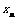 ,且
,且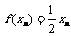 .
.
(Ⅰ)数列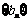 和
和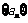 的通项公式;
的通项公式;
(Ⅱ)求证: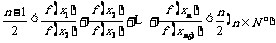 .
.
[答案及详细解析]
20.(本小题满分14分)在直角坐标平面上,O为原点,M为动点,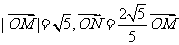 . 过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
. 过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,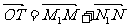 . 记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
. 记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在直线l,使得|BP|=|BQ|,并说明理由.
19.(本小题满分14分)2008年北京奥运会中国跳水梦之队取得了辉煌的成绩. 据科学测算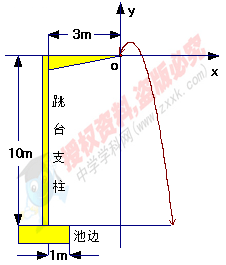 ,跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动轨迹(如图所示)是一经过坐标原点的抛物线(图中标出数字为已知条件),
,跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动轨迹(如图所示)是一经过坐标原点的抛物线(图中标出数字为已知条件),
且在跳某个规定的翻腾动作时,正常情况下运动员在空
中的最高点距水面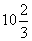 米,入水处距池边4米,同时
米,入水处距池边4米,同时
运动员在距水面5米或5米以上时,必须完成规定的
翻腾动作,并调整好入水姿势,否则就会出现失误.
(Ⅰ)求这个抛物线的解析式;
(Ⅱ)在某次试跳中,测得运动员在空中的运动轨迹
为(Ⅰ)中的抛物线,且运动员在空中调整好入水姿势时
距池边的水平距离为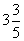 米,问此次跳水会不会失误?
米,问此次跳水会不会失误?
请通过计算说明理由;
(Ⅲ)某运动员按(Ⅰ)中抛物线运行,要使得此次跳水成功,他在空中调整好入水姿势时,距池边的水平距离至多应为多大?
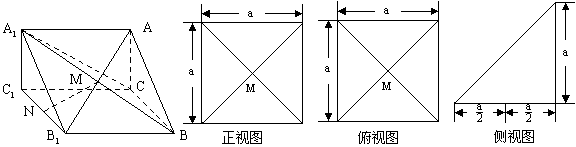
18.(本小题满分13分)如图,分别是直三棱柱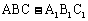 直观图及其正视图、俯视图、侧视图.
直观图及其正视图、俯视图、侧视图.
(Ⅰ)求证: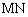 ∥平面
∥平面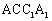 ;
;
(Ⅱ)求证: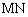 ⊥平面
⊥平面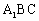 ;
;
(Ⅲ)求二面角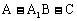 的大小.
的大小.
17.(本小题满分12分)为深入贯彻素质教育,增强学生体质,某中学从高一、高二、高三三个年级中分别选了甲、乙、丙三支足球队举办一场足球赛。足球赛具体规则为:甲、乙、丙三支足球队进行单循环赛(即每两个队比赛一场).共赛三场,每场比赛胜者积3分,负者积0分,没有平局.在每一场比赛中,甲胜乙的概率为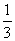 ,甲胜丙的概率为
,甲胜丙的概率为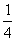 ,乙胜丙的概率为
,乙胜丙的概率为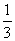 .
.
(Ⅰ)求甲队获得第一名且丙队获得第二名的概率;
(Ⅱ)设在该次比赛中,甲队积分为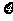 ,求
,求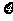 的分布列和数学期望.
的分布列和数学期望.
16.(本小题满分13分)已知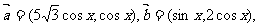 设函数
设函数
(Ⅰ)当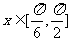 ,求函数
,求函数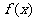 的的值域;
的的值域;
|
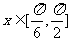 时,若
时,若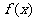 =8, 求函数
=8, 求函数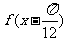 的值;
的值;
(Ⅲ)将函数y=f(x)的图象向右平移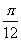 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数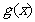 的表达式并判断奇偶性.
的表达式并判断奇偶性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com