
19. (本小题满分14分)
解:(Ⅰ)易知M的轨迹是椭圆, ,方程为
,方程为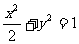 . -------3分
. -------3分
(Ⅱ)①当斜率存在时,设 ,由
,由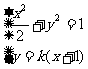 ,消去
,消去 整理得
整理得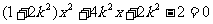 ;
-------5分
;
-------5分
设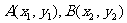 ,则有
,则有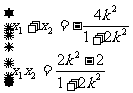 ………………① -------6分
………………① -------6分
以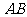 为直径的圆的方程为
为直径的圆的方程为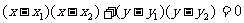 ,即
,即
 ;…………② -------7分
;…………② -------7分
由①得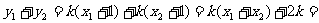
 ,……③
,……③
 ;……④
-------8分
;……④
-------8分
将①③④代入②化简得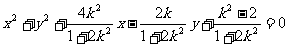 ,
,
即 .
-------10分
.
-------10分
对任意的 ,圆心
,圆心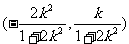 到直线
到直线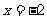 的距离是
的距离是 ,
,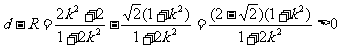 ,即
,即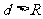 ,所以圆于直线相离.
-------12分
,所以圆于直线相离.
-------12分
当斜率不存在时,易得半径为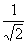 ,圆的方程是
,圆的方程是 ,与直线
,与直线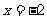 也相离.
-------14分
也相离.
-------14分
18. (本小题满分13分)
解:(Ⅰ)连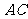 、
、 ,则
,则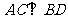 ;
;
∵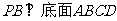 ,则
,则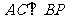 ,∴
,∴ .
.
而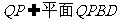 ,∴
,∴ .
-----------------------------4分
.
-----------------------------4分
(Ⅱ) 设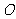 是
是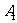
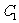 与
与
 的交点,
的交点,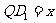 、
、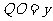 ,则
,则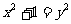 ,
,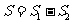
=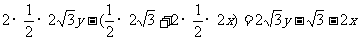
 .
-------------------8分
.
-------------------8分
∵令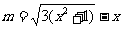 ,则
,则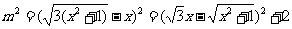 ,
,
∴当 即
即 时,
时,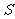 取得最小值.
-------------------11分
取得最小值.
-------------------11分
此时,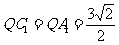 ,由余弦定理有
,由余弦定理有 ∠
∠
 .
.
-------------------13分
17. (本小题满分12分)
解:(Ⅰ)由 表示事件“购买该商品的3位顾客中至少有1位采用1期付款”,
表示事件“购买该商品的3位顾客中至少有1位采用1期付款”,
知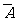 表示事件“购买该商品的3位顾客中无人采用1期付款” .
表示事件“购买该商品的3位顾客中无人采用1期付款” .
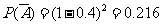 ,
, .…………4分
.…………4分
(Ⅱ) 的可能取值为
的可能取值为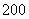 元,
元,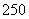 元,
元,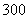 元.
元.
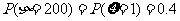 ,
,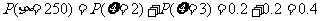 ,
,
 .
.
 的分布列为
的分布列为

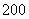
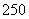
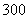

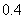
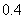
……………………10分
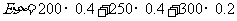
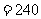 (元).……………………12分
(元).……………………12分
16. (本小题满分13分)
解:假设经过 小时在N处追上海盗船.在
小时在N处追上海盗船.在 中,
中, =5,
=5,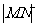 =20
=20 ,
, =30
=30 ,
,
∠ =
= .-----------------------------4分
.-----------------------------4分
由余弦定理有 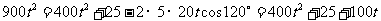 ,---7分
,---7分
化简得 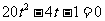 ,解之得
,解之得 >0,∴快艇能追上海盗船. --------10分
>0,∴快艇能追上海盗船. --------10分
由正弦定理有
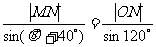 ,∴
,∴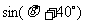
 .----------13分
.----------13分
(二)选做题(13-15题,考生只能从中选做两题)
13. 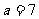 .解析:曲线C是圆,即
.解析:曲线C是圆,即 ,圆心是
,圆心是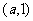 ,所以
,所以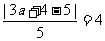 ,又
,又 ,所以
,所以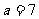 .
.
14.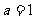 .解析:∵
.解析:∵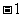 <
< <1,∴
<1,∴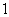 <
<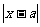 <3,
<3,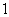 <
<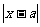 且
且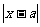 <3.由
<3.由 >1或
>1或
 <
<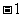 有
有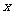 >
>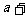 1或
1或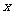 <
<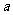
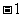 ;由
;由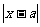 <3有
<3有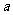 -3<
-3<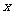 <
<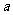 +3;而
+3;而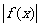 <1的解
<1的解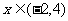 ,∴
,∴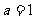 .
.
15. 110°.解析:∵ ,
,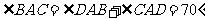 ,从而
,从而 ,∴
,∴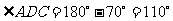 .
.
 (一)必做题(9-12题)
(一)必做题(9-12题)
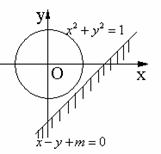
9.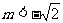 .解析:如图,
.解析:如图,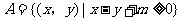 表示直线
表示直线 及其下方区域,
及其下方区域, 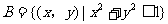 表示圆
表示圆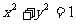 及内部,要使
及内部,要使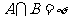 ,则直线
,则直线 在圆
在圆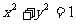 的下方, 即
的下方, 即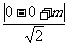 <
<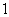 ,故
,故 .
.
10. .解析:依题意知,当
.解析:依题意知,当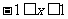 时,
时,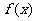 >0;此时若
>0;此时若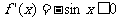 ,则
,则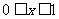 .
.
11.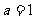 或
或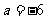 .解析:若
.解析:若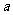 ﹥0,则函数图象对称轴是
﹥0,则函数图象对称轴是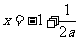 ,最大值是
,最大值是 ,
,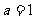 ;若
;若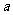 <0,最大值是
<0,最大值是 ,
,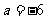 .
.
12.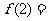 4,
4, .解析:易知2个圆周最多把平面分成4片;
.解析:易知2个圆周最多把平面分成4片;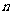 个圆周已把平面分成
个圆周已把平面分成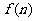 片,再放入第
片,再放入第 个圆周,为使得到尽可能多的片,第
个圆周,为使得到尽可能多的片,第 个应与前面
个应与前面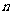 个都相交且交点均不同,有条公共弦,其端点把第
个都相交且交点均不同,有条公共弦,其端点把第 个圆周分成
个圆周分成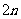 段,每段都把已知的某一片划分成2片,即
段,每段都把已知的某一片划分成2片,即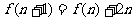 (
(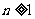 ),所以
),所以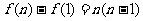 ,而
,而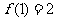 ,从而
,从而 .
.
8.C.解析:设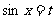 ,则
,则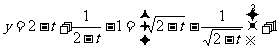 ;令
;令 ,
,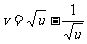 ,则
,则 .
. 是关于
是关于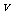 的二次函数,其图象关于直线
的二次函数,其图象关于直线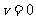 对称;但
对称;但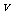 是关于
是关于 的增函数,而
的增函数,而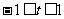 ,从而
,从而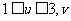 ﹥0,所以
﹥0,所以 是关于
是关于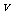 的的增函数,于是
的的增函数,于是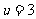 时,
时, .
.
第Ⅱ卷 非选择题 (共110分)
7.D.解析:设|PF1|=m, |PF2|=n,不妨设P在第一象限,则由已知得
 5a2-6ac+c2=0
5a2-6ac+c2=0 e2-6e+5=0,解得e=5或e=1(舍去),选D.
e2-6e+5=0,解得e=5或e=1(舍去),选D.
6. A.解析:设购买铅笔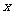 只,购买圆珠笔
只,购买圆珠笔 只,则
只,则 满足
满足 ,则
,则 为支出的钱数,易知,答案是A.
为支出的钱数,易知,答案是A.
5.D.解析: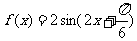 ,最小正周期是
,最小正周期是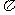 ,在
,在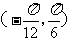 是增函数.
是增函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com