
19.解:(Ⅰ)易知,椭圆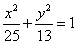 的半焦距为:
的半焦距为: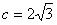 ,……..1分
,……..1分
又抛物线 的准线为:
的准线为: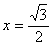 . ……..2分
. ……..2分
设双曲线M的方程为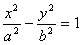 ,依题意有
,依题意有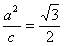 ,……..3分
,……..3分
故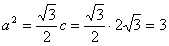 ,又
,又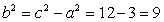 .……..4分
.……..4分
∴双曲线M的方程为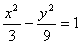 . ……..5分
. ……..5分
(Ⅱ)设直线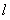 与双曲线M的交点为
与双曲线M的交点为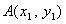 、
、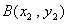 两点
两点
联立方程组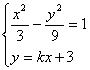 消去y得
消去y得 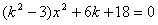 ,……..7分
,……..7分
∵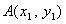 、
、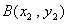 两点的横坐标是上述方程的两个不同实根,
两点的横坐标是上述方程的两个不同实根,
∴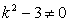 ……..8分
……..8分
∴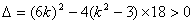
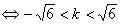 ,从而有
,从而有
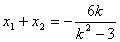 ,
,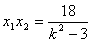 .……..9分
.……..9分
又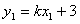 ,
,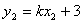
∴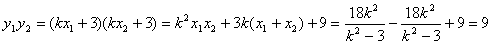
…...…...…...…..…...…...…...…..11分
若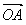
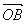
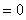 ,则有
,则有 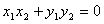 ,即
,即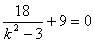
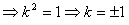 .
.
∴当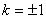 时,使得
时,使得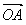
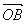
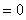 . ……..13分
. ……..13分
20解:(1)S1=a1=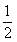 ,∴
,∴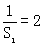
当n≥2时,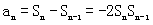 ,∴
,∴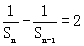
∴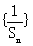 为等差数列,首项为2,公差为2………………………………(4分)
为等差数列,首项为2,公差为2………………………………(4分)
(2)由(1)知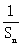 =2+(n-1)×2=2n,∴
=2+(n-1)×2=2n,∴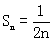 ……………………………………(6分)
……………………………………(6分)
当n≥2时,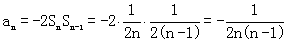
∴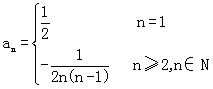 ………………………………………(9分)
………………………………………(9分)
(3) 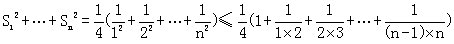
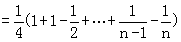
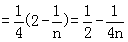 ………………(13分)
………………(13分)
17.解:(1)PC=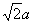 ,PD=PC=a,∴DPDC是RtD,且PD⊥DC,
,PD=PC=a,∴DPDC是RtD,且PD⊥DC,
同理PD⊥AD,又AD∩DC=D, ∴PD⊥平面ABCD。
(2)连BD,因ABCD是正方形,∴BD⊥AC,又PD⊥平面ABCD。
BD是PB在面ABCD上的射影,由三垂线定理得PB⊥AC,∴PB与AC成90°角。
(3)设AC∩BD=O,作AE⊥PB于E,连OE,
∵AC⊥BD,又PD⊥平面ABCD,ACÌ平面ABCD,∴PD⊥AC,
又PD∩BD=D, ∴AC⊥平面PDB,则OE是AE在平面PDB上的射影。
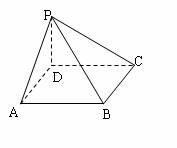 由三垂线定理逆定理知OE⊥PB, ∴ÐAEO是二面角A-PB-D的平面角。
由三垂线定理逆定理知OE⊥PB, ∴ÐAEO是二面角A-PB-D的平面角。
又AB=a,PA=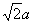 ,PB=
,PB=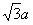 , ∵PD⊥平面ABCD,DA⊥AB,
, ∵PD⊥平面ABCD,DA⊥AB,
∴PA⊥AB,在RtDPAB中,AE•PB=PA•AB。∴AE=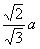 ,又AO=
,又AO=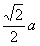
∴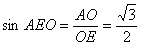 ,ÐAEO=60°,二面角A-PB-D的大小为60°。
,ÐAEO=60°,二面角A-PB-D的大小为60°。
18解:(I)只进行两局比赛,甲就取得胜利的概率为:
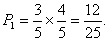 …………4分
…………4分
(II)只进行两局比赛,比赛就结束的概率为:
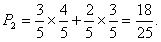 …………8分
…………8分
(III)甲取得比赛胜利共有三种情形:
若甲胜乙,甲胜丙,则概率为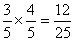 ;
;
若甲胜乙,甲负丙,则丙负乙,甲胜乙,概率为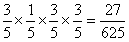 ;
;
若甲负乙,则乙负丙,甲胜丙,甲胜乙,概率为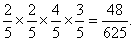
所以,甲获胜的概率为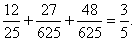
16.解:(1)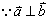 ,
, 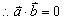 .
.
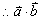
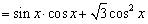
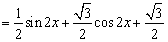
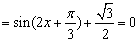
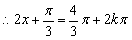 或
或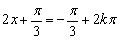 ,
,
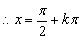 或
或 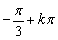 .
.
所求解集为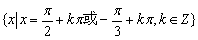
(2)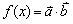
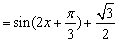 ,
,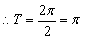 .
.
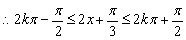 ,原函数增区间为
,原函数增区间为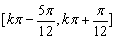
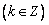
15. 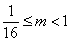
14. 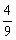
13. 0
12. 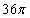
11.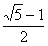
21.(本小题满分13分)已知是实数,函数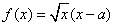 .
.
⑴求函数f(x)的单调区间;
⑵设g()为f(x)在区间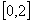 上的最小值.
上的最小值.
(i)写出g()的表达式;(ii)求的取值范围,使得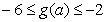 .
.
2009-2010学年度十堰市部分重点中学高三年级10月调考
20. (本小题满分13分)已知数列{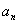 }的前n项和为
}的前n项和为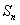 ,且满足
,且满足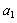 =
=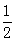 ,
,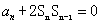 (n≥2).
(n≥2).
(1)判断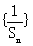 是否为等差数列?并证明你的结论;
是否为等差数列?并证明你的结论;
(2)求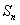 和
和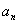 ;
;
(3)求证: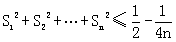 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com