
2.若 ,则
,则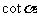 =____________
=____________
1.函数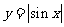 的一个单调增区间是( )
的一个单调增区间是( )
A.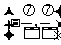 B.
B.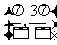 C.
C.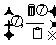 D.
D.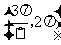
9.[答案]解:(1)线段PG与PC的位置关系是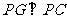 ;
;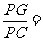
 .
.
(2)猜想:(1)中的结论没有发生变化.
证明:如图,延长GP交AD于点H,连结CH和CG.
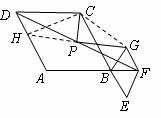
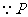 是线段
是线段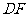 的中点,
的中点,
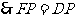 .
.
由题意可知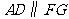 .
.
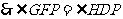 .
.
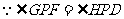 ,
,
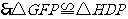 .
.
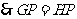 ,
,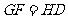 .
.
 四边形
四边形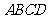 是菱形,
是菱形,
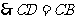 ,
,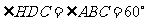 .
.
由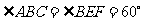 ,且菱形
,且菱形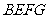 的对角线
的对角线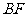 恰好与菱形
恰好与菱形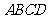 的边
的边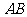 在同一条直线上,
在同一条直线上,
可得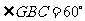 .
.
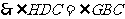 .
.
 四边形
四边形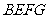 是菱形,
是菱形,
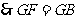 .
.
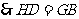 .
.
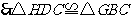 .
.
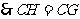 ,
,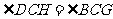 .
.
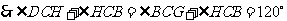 .
.
即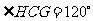 .
.
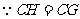 ,
,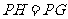 ,
,
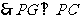 ,
,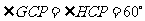 .
.
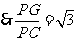 .
.
(3)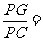
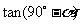 .
.
8.[解析]这是函数与圆相结合的综合题.解决这样的综合题,不光要把握题设条件,还要善于识别图象提供的条件.象这道题中的横轴,纵轴互相垂直,点A,B,D的坐标,蛋圆的圆心位置,同学们在解题时都要结合图形去发掘.
[答案]解:(1)解法1:根据题意可得:A(-1,0),B(3,0);
则设抛物线的解析式为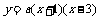 (a≠0)
(a≠0)
又点D(0,-3)在抛物线上,∴a(0+1)(0-3)=-3,
解之得:a=1 ∴y=x2-2x-3自变量范围:-1≤x≤3
解法2:设抛物线的解析式为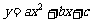 (a≠0)
(a≠0)
根据题意可知,A(-1,0),B(3,0),D(0,-3)三点
都在抛物线上∴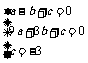 ,解之得:
,解之得:
∴y=x2-2x-3 自变量范围:-1≤x≤3
(2)设经过点C“蛋圆”的切线CE交x轴于点E,
连结CM,在Rt△MOC中,∵OM=1,CM=2,
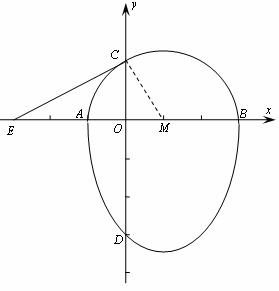
∴∠CMO=60°,OC=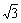
在Rt△MCE中,∵CM=2,∠CMO=60°,∴ME=4
∴点C、E的坐标分别为(0,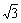 ),(-3,0)
),(-3,0)
∴切线CE的解析式为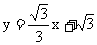
(3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0)
由题意可知方程组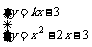 只有一组解 即
只有一组解 即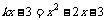 有两个相等实根,∴k=-2
有两个相等实根,∴k=-2
∴过点D“蛋圆”切线的解析式y=-2x-3
6.[解析]这一类型题目关键是看懂题目,按照题目的要求去做即可.
[答案]模型拓展一:(1)1+5=6;(2)1+5×9=46;(3)1+5(n-1)
模型拓展二:(1)1+m;(2)1+m(n-1)
问题解决:(1)在不透明口袋中放入18种颜色的小球(小球除颜色外完全相同)各40个,现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
(2)1+18×(10-1) =163
4.[解析]本题考查了二次根式的性质及数学的分类思想,可以模仿例题,当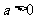 时,令a=9,则
时,令a=9,则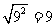 ,当
,当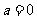 时,令a=0,则
时,令a=0,则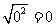 ,当
,当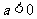 时,如
时,如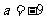 则
则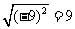 ,很容易得出答案。
,很容易得出答案。
[答案](1)写出类似例的文字描述

(2)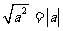
3.[解析]按照题目给出的转化方法将行列式转化为方程, 在解分式方程的时候要注意检验.
[答案]解: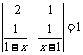
整理得:2×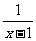 -
-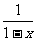 =1
=1
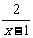 +
+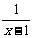 =1
=1
解之得:x=4
2.[解析]本题是信息的使用,对给出的信息准确的分析,模仿使用即可.箭头所指数的相反数.注意运算顺序. 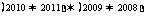 =(-2011)
=(-2011) (-)=2011
(-)=2011
[答案]2011
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com