
3.通项公式法:利用等差数列得通项公式是关于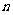 的一次函数这一性质。
的一次函数这一性质。
例五 设数列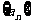 其前
其前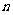 项和
项和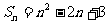 ,问这个数列成AP吗?
,问这个数列成AP吗?
解: 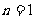 时
时 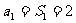
 时
时 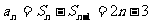
∵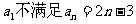 ∴
∴ 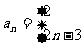
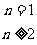
∴ 数列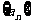 不成AP 但从第2项起成AP。
不成AP 但从第2项起成AP。
2.中项法: 即利用中项公式,若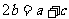 则
则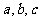 成AP。
成AP。
例四 《课课练》第4 课 例一
已知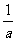 ,
,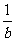 ,
,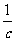 成AP,求证
成AP,求证 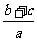 ,
,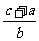 ,
,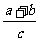 也成AP。
也成AP。
证明: ∵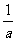 ,
,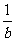 ,
,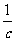 成AP ∴
成AP ∴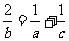 化简得:
化简得: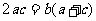
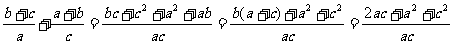
=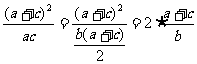
∴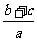 ,
,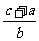 ,
,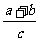 也成AP
也成AP
1.定义法:即证明 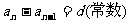
例三 《课课练》第3课 例三
已知数列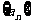 的前
的前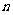 项和
项和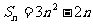 ,求证数列
,求证数列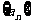 成等差数列,并求其首项、公差、通项公式。
成等差数列,并求其首项、公差、通项公式。
解: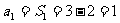
当 时
时 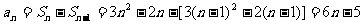
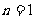 时 亦满足 ∴
时 亦满足 ∴ 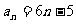
首项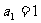
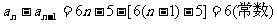
∴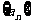 成AP且公差为6
成AP且公差为6
求证:1°
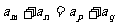 2°
2° 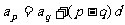
证明:1° 设首项为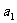 ,则
,则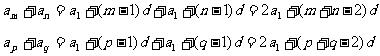
∵ 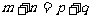 ∴
∴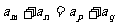
2° ∵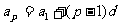
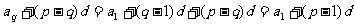
∴ 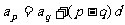
注意:由此可以证明一个定理:设成AP,则与首末两项距离相等的两项和等于首末两项的和 ,即: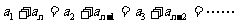
同样:若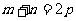 则
则 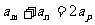
例二 在等差数列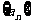 中,
中,
1°
若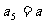
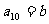 求
求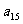
解: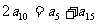 即
即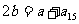 ∴
∴ 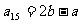
2° 若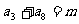 求
求 
解: =
=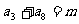
3°
若 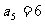
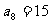 求
求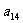
解: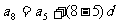 即
即 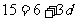 ∴
∴ 
从而 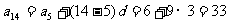
4°
若 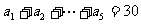
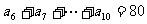 求
求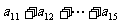
解:∵ 6+6=11+1 7+7=12+2 ……
∴ 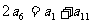
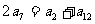 ……
……
从而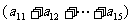 +
+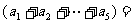 2
2
∴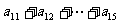 =2
=2 -
-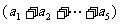
=2×80-30=130
2. 计算:
①  ②
②
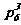 ③
③
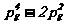 ④
④

1. 写出:
① 从五个元素a、b、c、d、e中任意取出两个、三个元素的所有排列;
② 由1、2、3、4组成的无重复数字的所有3位数.
③ 由0、1、2、3组成的无重复数字的所有3位数.
2. 排列数公式: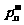 =n(n-1)(n-2)…(n-m+1)
=n(n-1)(n-2)…(n-m+1)
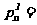 ;
;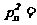 ;
; ;
;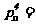 ;
;
计算: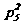 =
;
=
; 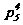 = ;
= ;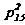 =
;
=
;
[课后检测]
1. 定义:从n个不同元素中,任取m(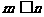 )个元素的所有排列的个数叫做从n个元素中取出m元素的排列数,用符号
)个元素的所有排列的个数叫做从n个元素中取出m元素的排列数,用符号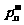 表示.
表示.
用符号表示上述各题中的排列数.
2.已知a、b、c、d四个元素,①写出每次取出3个元素的所有排列;②写出每次取出4个元素的所有排列.
[排列数]
1. 由数字1、2、3、4可以组成多少个无重复数字的三位数?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com