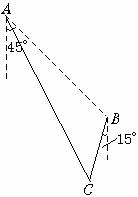
12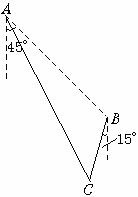．甲舰在A处，乙舰在A的南偏东45°方向，距A有9 nmile，并以20 nmile/h的速度沿南偏西15°方向行驶，若甲舰以28 nmile/h的速度行驶，应沿什么方向，用多少时间，能尽快追上乙舰？

解：设th甲舰可追上乙舰，相遇点记为C

则在△ABC中，AC＝28t，BC＝20t，AB＝9，∠ABC＝120°

由余弦定理

AC²＝AB²+BC²－2AB·BCcosABC

(28t)²＝81+(20t)²－2×9×20t×(－)

整理得128t²－60t－27＝0

解得t＝　(t＝－舍去)

故BC＝15(nmile)，AC＝21( nmile)

由正弦定理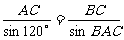

∴sinBAC＝×＝

∠BAC＝arcsin

故甲舰沿南偏东－arcsin的方向用0.75 h可追上乙舰.

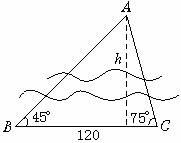
11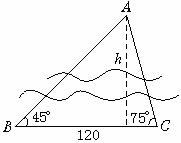．欲测河的宽度，在一岸边选定A、B两点，望对岸的标记物C，测得∠CAB＝45°，∠CBA＝75°，AB＝120 m，求河宽.(精确到0.01 m)

解：由题意C＝180°－A－B＝180°－45°－75°＝60°

在△ABC中，由正弦定理＝

∴ BC＝＝＝＝40

S_△ABC＝AB·BCsinB＝AB·h

∴h＝BCsinB＝40×＝60+20≈94.64

∴河宽94.64米.

10．在△ABC中，求证：－＝－.

提示：左边＝－＝(－)－2(－)＝右边.

9．15

1．C　 2．B　 3．D　 4．C　 5．东南　 a　 6．40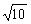　 7．10　8．20，

12．甲舰在A处，乙舰在A的南偏东45°方向，距A有9 nmile，并以20 nmile/h的速度沿南偏西15°方向行驶，若甲舰以28 nmile/h的速度行驶，应沿什么方向，用多少时间，能尽快追上乙舰？

解三角形应用举例答案

11．欲测河的宽度，在一岸边选定A、B两点，望对岸的标记物C，测得∠CAB＝45°，∠CBA＝75°，AB＝120 m，求河宽.(精确到0.01 m)

10．在△ABC中，求证：－＝－.

9．在塔底的水平面上某点测得塔顶的仰角为θ，由此点向塔沿直线行走30米，测得塔顶的仰角为2θ，再向塔前进10米，又测得塔顶的仰角为4θ，则塔高是　　　　 米.　

8．甲、乙两楼相距20 m，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30⁰，则甲、乙两楼的高分别是　　　　 .