
9.若 为偶函数,
为偶函数,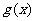 为奇函数,且
为奇函数,且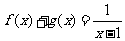 ,则
,则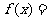
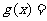
8.已知 为
为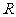 上的奇函数,当
上的奇函数,当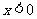 时,
时,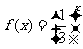 ,那么
,那么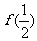 =
=
7.已知函数 是定义在
是定义在 上的偶函数.当
上的偶函数.当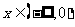 时,
时,
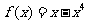 ,则当
,则当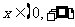 时,
时,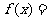
热点考向一:一般函数的奇偶性判断
例1.判断下列各函数的奇偶性:
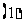
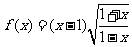 ;
;
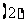
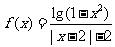 ;
;
(3)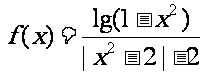 (4)
(4)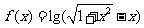
(5)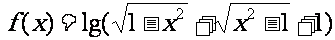
(6) 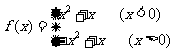
热点考向二:分段函数的奇偶性
例2. 已知
已知 是
是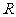 上的奇函数,且当
上的奇函数,且当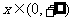 时,
时,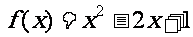 ,
,
则 的解析式为
的解析式为
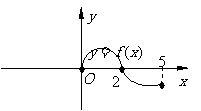
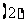 设奇函数
设奇函数 的定义域为
的定义域为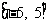 若当
若当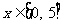 时,
时,
 的图象如右图,则不等式
的图象如右图,则不等式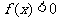 的解是
的解是
热点考向三:抽象函数的奇偶性
例3.(1)已知函数 满足:
满足: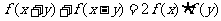 对任意的实数
对任意的实数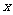 、
、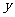 总成立,且
总成立,且 .求证:
.求证: 为偶函数.
为偶函数.
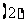 设定义在
设定义在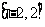 上的偶函数
上的偶函数 在区间
在区间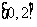 上单调递减,若
上单调递减,若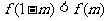 ,
,
求实数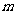 的取值范围
的取值范围
热点考向四:函数奇偶性与单调性的综合应用
例4.函数f(x)的定义域为D={x|x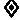 0},且满足对于任意x1,x2
0},且满足对于任意x1,x2 D,f(x1·x2)=f(x1)+f(x2)
D,f(x1·x2)=f(x1)+f(x2)
(1) 求f(1)的值
(2) 判断f(x)的奇偶性并证明你的结论
(3) 若f(4)=1,f(3x+1)+f(2x-6) 3,且f(x)在
3,且f(x)在 上是增函数,求x的取值范围。
上是增函数,求x的取值范围。
五当堂检测
 已知函数
已知函数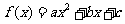 ,
,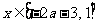 是偶函数,则
是偶函数,则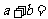
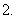 已知
已知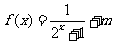 为奇函数,则
为奇函数,则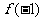 的值为
的值为
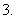 已知
已知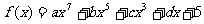 ,其中
,其中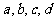 为常数,若
为常数,若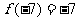 ,
,
则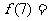
 若函数
若函数 是定义在
是定义在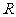 上的奇函数,则函数
上的奇函数,则函数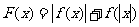 的图象关于
的图象关于
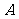
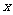 轴对称
轴对称 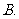
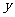 轴对称
轴对称 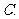 原点对称
原点对称 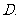 以上均不对
以上均不对
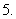 函数
函数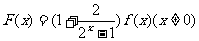 是偶函数,且
是偶函数,且 不恒等于零,则
不恒等于零,则 (
)
(
)
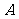 是奇函数
是奇函数
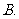 是偶函数
是偶函数
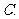 可能是奇函数也可能是偶函数
可能是奇函数也可能是偶函数 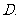 不是奇函数也不是偶函数
不是奇函数也不是偶函数
6.已知函数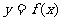 在
在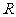 是奇函数,且当
是奇函数,且当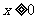 时,
时,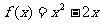 ,则
,则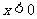 时,
时,
 的解析式为
的解析式为
5.(09重庆理)若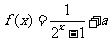 是奇函数,则
是奇函数,则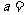 .
.
4.(09陕西卷文)定义在R上的偶函数 满足:对任意的
满足:对任意的 ,有
,有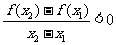 .则f(3),f(-2),f(1)三者大小的关系为
.则f(3),f(-2),f(1)三者大小的关系为
3.(09辽宁文)已知偶函数 在区间
在区间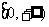 单调增加,则满足
单调增加,则满足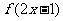 <
<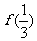 的x 取值范围是
的x 取值范围是
2.(09四川文)已知函数 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数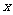 都有
都有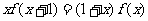 ,则
,则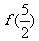 =
=
1.(09江西文)已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有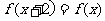 ,且当
,且当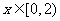 时,
时,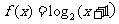 ,则
,则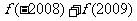 =
=
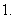 函数的奇偶性的定义:设
函数的奇偶性的定义:设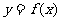 ,
,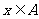 ,如果对于任意
,如果对于任意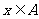 ,都有_________,则称函数
,都有_________,则称函数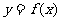 为奇函数;如果对于任意
为奇函数;如果对于任意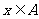 ,都有_________,则称函数
,都有_________,则称函数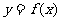 为偶函数;
为偶函数;
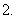 奇偶函数的性质:
奇偶函数的性质:
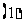 函数具有奇偶性的必要条件:_________
函数具有奇偶性的必要条件:_________
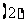
 是偶函数
是偶函数
 的图象_________;
的图象_________;
 是奇函数
是奇函数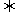
 的图象关于_________;
的图象关于_________;
 奇函数在对称的单调区间内有_________的单调性,偶函数在对称的单调区间内具有_________的 单调性.
奇函数在对称的单调区间内有_________的单调性,偶函数在对称的单调区间内具有_________的 单调性.
(4) 为偶函数
为偶函数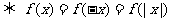 .
.
(5)若奇函数 的定义域包含
的定义域包含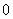 ,则_________.
,则_________.
3.判断函数的奇偶性的方法:
 定义法:首先判断其定义域是否关于原点中心对称. 若不对称,则为非奇非偶函数;若对称,则再判断
定义法:首先判断其定义域是否关于原点中心对称. 若不对称,则为非奇非偶函数;若对称,则再判断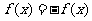 或
或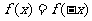 是否定义域上的恒等式;
是否定义域上的恒等式;
 图象法;
图象法;
 性质法:①设
性质法:①设 ,
,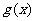 的定义域分别是
的定义域分别是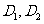 ,那么在它们的公共定义域
,那么在它们的公共定义域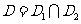 上:奇
上:奇 奇
奇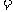 奇,偶
奇,偶 偶
偶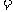 偶,奇
偶,奇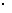 奇
奇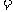 偶,偶
偶,偶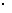 偶
偶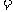 偶,奇
偶,奇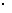 偶
偶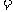 奇;
奇;
②若某奇函数若存在反函数,则其反函数必是奇函数;
 判断函数的奇偶性有时可以用定义的等价形式:
判断函数的奇偶性有时可以用定义的等价形式: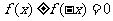 ,
,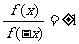
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com