
4.A[解析]由题意得函数f(x)关于直线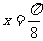 对称,所以
对称,所以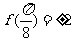 ,故选A.
,故选A.
[链接高考]三角函数是高中数学的必修内容,主要有三角变换、三角函数图象和性质、解三角形,是高考必考内容,属于容易题.
3.C[解析]由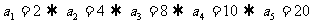 ,故选C.
,故选C.
[链接高考]数列是一种特殊函数,等差、等比数列是数列中的常用数列和常考内容.
2.B[解析]此题涉及到排列中的捆绑问题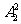 和计数原理中的分步得
和计数原理中的分步得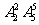 ,故选B.
,故选B.
[链接高考]计数原理是高中数学中理科选修内容,能反映学生的抽象思维,是重要知识之一.
1.B[解析]由题意知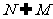 ,所以
,所以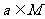 不一定能得到
不一定能得到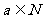 ,但
,但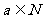 一定得到
一定得到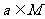 ,由此得到答案B.
,由此得到答案B.
[链接高考]集合是高中数学的基本概念之一,它与不等式、充要条件或其他任何知识联系起来,属于容易题.
21.(本小题满分14分)
已知数列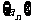 满足条件
满足条件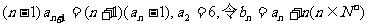
(Ⅰ)写出数列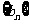 的前四项;
的前四项;
(Ⅱ)求数列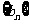 的通项公式,并给出证明;
的通项公式,并给出证明;
(Ⅲ)是否存在非零常数p,q,使得数列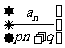 成等差数列?若存在,求出p,q满足的关系式;若不存在,说明理由.
成等差数列?若存在,求出p,q满足的关系式;若不存在,说明理由.
[答案及详细解析]
20.(本小题满分14分)
已知椭圆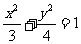 的焦点F与抛物线C:
的焦点F与抛物线C: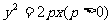 的焦点关于直线x-y=0对称.
的焦点关于直线x-y=0对称.
(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab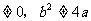 ),M是抛物线C上的点,设直线AM,BM与抛物线的另一交点为
),M是抛物线C上的点,设直线AM,BM与抛物线的另一交点为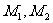 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要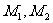 存在且
存在且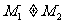 )直线
)直线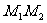 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.
19.(本小题满分13分)
在军训期间,某校学生进行实弹射击.
(Ⅰ)通过抽签,将编号为1~6的六名同学排到1~6号靶位,试求恰有3名同学所抽靶位号与其编号相同的概率;
(Ⅱ)此次军训实弹射击每人射击三次,总环数不少于28环的同学可获得射击标兵称号.已知某同学击中10环、9环、8环的概率分别为0.1、0.2、0.2,求该同学能获得射击标兵称号的概率.
18. (本小题满分14分)
(本小题满分14分)
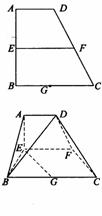
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=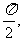
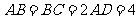 ,E、F分别是AB、CD上的中点,
,E、F分别是AB、CD上的中点,
G是BC的中点. 沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).
(Ⅰ)求证:BD⊥EG;
(Ⅱ)(2)求EG和平面ABCD所成的角;
(Ⅲ)求二面角B-DC-F的余弦值.
17.(本小题满分13分)
已知函数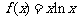 .
.
(Ⅰ)求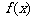 的最小值;
的最小值;
(Ⅱ)若对所有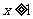 都有
都有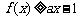 ,求实数
,求实数 的取值范围.
的取值范围.
16.(本小题满分12分)
已知x是三角形的内角,且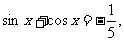
(Ⅰ)求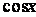 的值;
的值;
(Ⅱ)求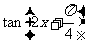 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com