
21.(13分)设函数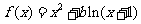 .①若对定义域内任意
.①若对定义域内任意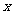 ,都有
,都有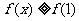 成立,求实数
成立,求实数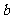 的值②若函数
的值②若函数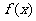 在定义域上是单调函数,求
在定义域上是单调函数,求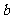 的范围;③若
的范围;③若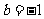 ,证明对任意正整数
,证明对任意正整数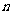 ,不等式
,不等式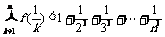 都成立.
都成立.
20.

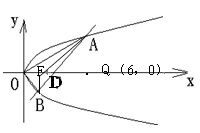
19.(13分)如图,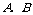 是抛物线
是抛物线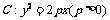 上的两个动点,
上的两个动点,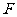 是焦点,直线
是焦点,直线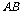 不垂直于
不垂直于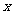 轴且交
轴且交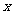 轴于点
轴于点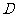 .(1)若
.(1)若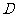 与
与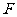 重合,且直线
重合,且直线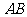 的倾斜角为
的倾斜角为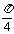 ,求证:
,求证: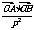 是常数(
是常数(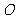 是坐标原点);(2)若
是坐标原点);(2)若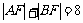 ,线段
,线段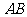 的垂直平分线恒过定点
的垂直平分线恒过定点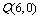 ,求抛物线
,求抛物线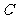 的方程;
的方程;
18、 (12分)如图,在直三棱柱
(12分)如图,在直三棱柱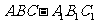 中,
中,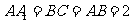 ,
,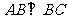 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。
(1)求二面角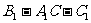 的大小。
的大小。
(2)证明:在AB上存在一个点Q,使得平面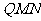 ⊥平面
⊥平面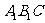 ,并求出
,并求出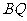 的长度。
的长度。
16.( 12分)已知A、B均为钝角,且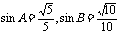 ,求A+B。
,求A+B。
17( 12分)在区间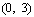 内随机取两数
内随机取两数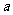 ,
,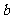 构造关于
构造关于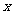 的二次方程
的二次方程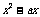
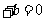 ,事件
,事件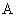 :“关于
:“关于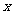 二次方程
二次方程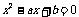 的两实根
的两实根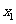 ,
,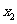 满足
满足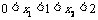 ”。(1)求事件
”。(1)求事件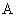 发生的概率
发生的概率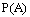 ;
;
(2)按上述方法相互独立地依次构造三个关于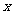 的二次方程,记这三个方程中使事件
的二次方程,记这三个方程中使事件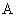 发生的个数为
发生的个数为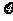 ,求随机变量
,求随机变量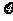 的分布列以及数学期望
的分布列以及数学期望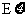 。
。
15. 给出下列四个命题:
①命题“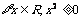 ”的否定是“
”的否定是“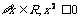 ”;②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;③若a,b
”;②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;③若a,b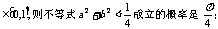 ④函数y=log
④函数y=log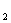 (x
(x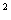 -ax+2)在
-ax+2)在 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是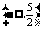 其中真命题的序号是
其中真命题的序号是
14.有10名同学先站成了前排3人后排7人来照毕业纪念像,但现在摄影师要从后排7人中抽2人
调整到前排,并使另外8个人的相对顺序不变,则不同调整方法的总数是 (用数字作答)
13.函数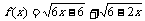 的最大值为
的最大值为
12. 若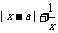 ≥
≥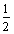 对一切x>0恒成立,则a的取值范围是
.
对一切x>0恒成立,则a的取值范围是
.
11. 甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、0.5,则三人都达标的概率是 ,三人中至少有一人达标的概率是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com