偶函数Û图象关于轴对称

3．

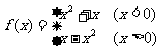
　解：显然定义域关于原点对称

　　 当 x>0时,　 -x<0　 f (-x) = x²-x = -(x-x²)

　　 当 x<0时,　 -x>0　 f (-x) = -x-x² = -(x²+x)

　　 即：

∴此函数为奇函数

2．

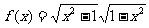
　解：定义域：　∴定义域为 x =±1

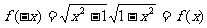　　 　　且　 f (±1) = 0

∴此函数为即奇且偶函数

1．

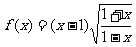
　解：定义域：　关于原点非对称区间

　　∴此函数为非奇非偶函数

此题系函数奇偶性与单调性综合例题，比例典型．

小结：一般函数的奇偶性有四种：奇函数、偶函数、即奇且偶函数、非奇非偶函数

　 　　　例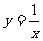：　　　 　y=2x　　 (奇函数)　　

　　　　 y=-3x²+1　　 y=2x⁴+3x²　 (偶函数)　

y=0　　　　　　　 (即奇且偶函数)

y=2x+1　　　　　 (非奇非偶函数)

4．得出奇(偶)函数的定义(见P61　略)

注意强调：①定义本身蕴涵着：

函数的定义域必须是关于原点的对称区间――这是奇(偶)函数的必要条件――前提

②＂定义域内任一个＂：

意味着不存在＂某个区间上的＂的奇(偶)函数――不研究

③判断函数奇偶性最基本的方法：

先看定义域，再用定义――f(-x)=f(x)　 ( 或f(-x)=-f(x) )

3．继而，更深入分析这两种对称的特点：

①当自变量取一对相反数时，y取同一值．

f(x)=y=x²　　 f(-1)=f(1)=1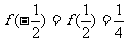　　

即 f(-x)=f(x)

再抽象出来：如果点 (x,y) 在函数y=x²的图象上，则该点关于y轴的对称点 (-x,y) 也在函数y=x²的图象上．

②当自变量取一对相反数时，y亦取相反数．

f(x)=y=x³ f(-1)=-f(1)=-1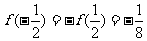　

即 f(-x)=f(x)

再抽象出来：如果点 (x,y) 在函数y=x³的图象上，则该点关于原点的对称点 (-x,-y) 也在函数y=x³的图象上．

1．依然观察 y=x²与 y=x³ 的图象――从对称的角度

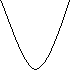
．观察结果：

y=x²的图象关于轴对称　　　

y=x³的图象关于原点对称

2．试用集合符号表示下列各语句，并画出图形：(1)点A在平面α内，但不在平面β内；(2)直线a经过不属于平面α的点A，且a不在平面α内；(3)平面α与平面β相交于直线l，且l经过点P；(4)直线l经过平面α外一点P，且与平面α相交于点M．