
6. After he retired from office, Rogers painting for a while, but soon lost interest.
A. took up B. saved up C. kept up D. drew up
5. Always read the on the bottle carefully and take the right amount of medicine.
A. explanations B. instructions C. descriptions D. introductions
4. Every time he to visit me, he buy me some books.
A. will come; will B. comes; will C. comes; would D. will come; would
3. Because of the young man’s English, he couldn’t make himself _______.
A. broken; understood B. broken; understand
C. break; understand D. breaking; understanding
2. Only in this way ______ our goals.
A. we can reach B. can we arrive C. we can arrive D. can we reach
从所给的四个选项(ABC和D)中,选出可以填入空白处的最佳选项。
1. Little Brown lives in _____ A-shaped house near the town. It is easy for him to attend
______ school.
A. the; 不填 B. 不填; a C. an; a D. an; 不填
21.(本题满分14分)
已知数列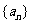 中,
中,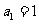 ,且
,且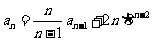
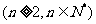 .
.
(Ⅰ) 求数列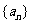 的通项公式;
的通项公式;
(Ⅱ) 令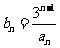
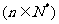 ,数列
,数列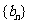 的前
的前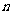 项和为
项和为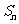 ,试比较
,试比较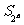 与
与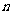 的大小;
的大小;
(Ⅲ) 令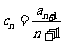
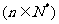 ,数列
,数列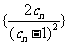 的前
的前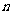 项和为
项和为 .求证:对任意
.求证:对任意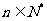 ,
,
都有  .
.
21解:(Ⅰ)由题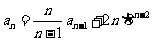 知,
知, 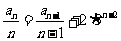 ,
,
由累加法,当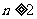 时,
时,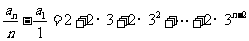
代入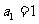 ,得
,得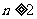 时,
时,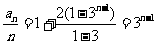
又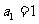 ,故
,故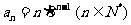 .
................4分
.
................4分
(II)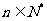 时,
时,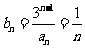 .
.
方法1:当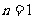 时,
时,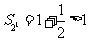 ;当
;当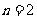 时,
时,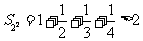 ;
;
当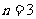 时,
时,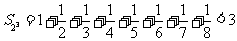 .
.
猜想当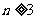 时,
时,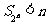 .
................6分
.
................6分
下面用数学归纳法证明:
①当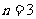 时,由上可知
时,由上可知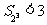 成立;
成立;
②假设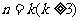 时,上式成立,即
时,上式成立,即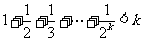 .
.
当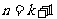 时,左边
时,左边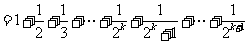
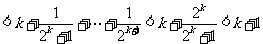 ,所以当
,所以当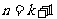 时成立.
时成立.

 由①②可知当
由①②可知当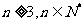 时,
时,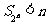 .
.
综上所述:当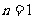 时,
时,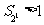 ;当
;当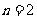 时,
时,  ;
;
当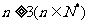 时,
时,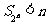 .
...............10分
.
...............10分
方法2: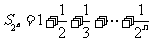
记函数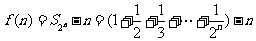
所以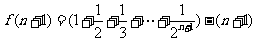 .........6分
.........6分
则
所以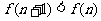 .
.
由于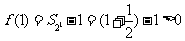 ,此时
,此时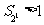 ;
;
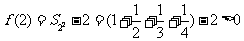 ,此时
,此时 ;
;
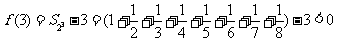 ,此时
,此时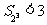 ;
;
由于,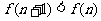 ,故
,故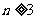 时,
时,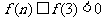 ,此时
,此时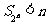 .
.
综上所述:当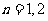 时,
时,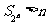 ;当
;当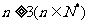 时,
时,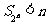 . ...........10分
. ...........10分
(III)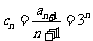
当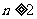 时,
时,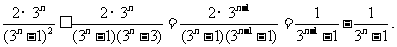
所以当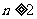 时
时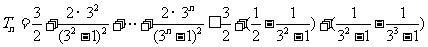
+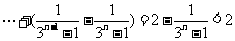 .
.
且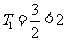
故对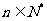 ,
, 得证.
.................14分
得证.
.................14分
20.(本题满分13分)
已知函数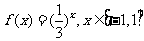 ,函数
,函数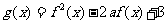 的最小值为
的最小值为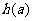 .
.
(1)求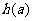 的解析式;
的解析式;
(2)是否存在实数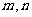 同时满足下列两个条件:①
同时满足下列两个条件:①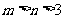 ;②当
;②当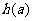 的定义域为
的定义域为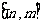 时,值域为
时,值域为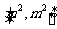 ?若存在,求出
?若存在,求出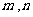 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
20解:(1)由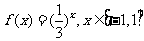 ,知
,知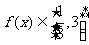 ,令
,令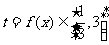
............1分
记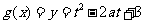 ,则
,则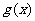 的对称轴为
的对称轴为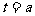 ,故有:
,故有:
①当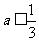 时,
时,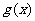 的最小值
的最小值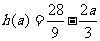
②当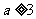 时,
时,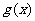 的最小值
的最小值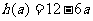
③当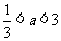 时,
时,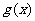 的最小值
的最小值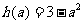
综述, ............7分
............7分
(2)当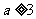 时,
时,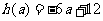 .故
.故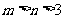 时,
时,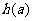 在
在 上为减函数.
上为减函数.
所以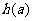 在
在 上的值域为
上的值域为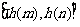 .
............9分
.
............9分
由题,则有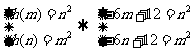 ,两式相减得
,两式相减得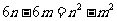 ,又
,又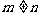
所以 ,这与
,这与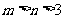 矛盾.故不存在满足题中条件的
矛盾.故不存在满足题中条件的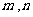 的值.
的值.
............13分
19.(本题满分12分)
已知二次函数 ,不等式
,不等式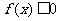 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列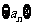 的前
的前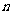 项和为
项和为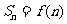 .
.
(1)求数列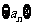 的通项公式;
的通项公式;
(2)设各项均不为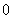 的数列
的数列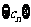 中,满足
中,满足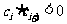 的正整数
的正整数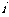 的个数称作数列
的个数称作数列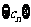 的变号数,令
的变号数,令 ,求数列
,求数列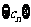 的变号数.
的变号数.
19解:(1)由于不等式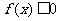 的解集有且只有一个元素,
的解集有且只有一个元素,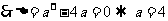
故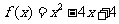 .
..................2分
.
..................2分
由题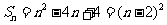
则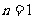 时,
时,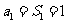 ;
;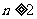 时,
时,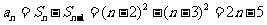
故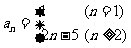 ...................6分
...................6分
(2)由题可得,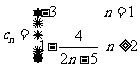
由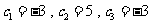 ,所以
,所以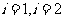 都满足
都满足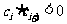 ..............8分
..............8分
当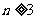 时,
时,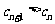 ,且
,且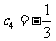 ,同时
,同时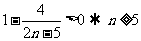 ,可知
,可知
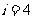 满足
满足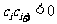 ;
;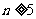 时,均有
时,均有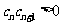 .
.
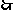 满足
满足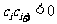 的正整数
的正整数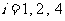 ,故数列
,故数列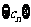 的变号数
的变号数 . ............12分
. ............12分
18.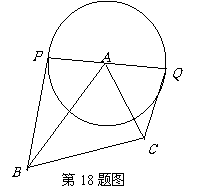 (本题满分12分)
(本题满分12分)
已知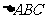 中,
中,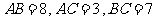 ,
,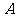 为圆心,直径
为圆心,直径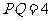 ,求
,求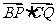 的最大值、最小值,并分别指出取得最值时
的最大值、最小值,并分别指出取得最值时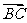 与
与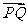 夹角的大小.
夹角的大小.
18解:在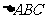 中,由余弦定理知
中,由余弦定理知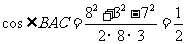 ,故
,故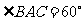 .
.
............3分
所以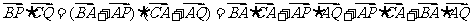
=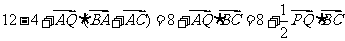 ..........7分
..........7分
故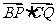 的最大值为
的最大值为 ,此时
,此时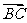 与
与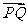 夹角为
夹角为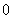 .
.
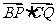 的最小值为
的最小值为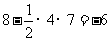 ,此时
,此时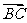 与
与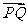 夹角为
夹角为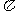 .
.........12分
.
.........12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com