
4.已知数列 的通项公式为
的通项公式为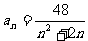 ,
,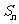 是数列
是数列 的前n项的和,则与
的前n项的和,则与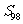 最接近的整数是
( )
最接近的整数是
( )
A. 24 B. 25 教育博客 C. 35 D. 36
2.已知函数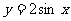 的定义域为
的定义域为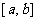 ,值域为[-2,1],则
,值域为[-2,1],则 的值不可能是
( )
的值不可能是
( )
A.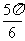 B.
B.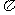 C.
C.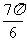 D.
D.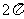
3. 已知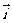 与
与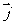 为互相垂直的单位向量,
为互相垂直的单位向量, ,
,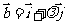 且
且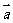 与
与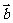 的夹角为锐角,则实数
的夹角为锐角,则实数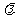 的取值范围是
( )
的取值范围是
( )
A.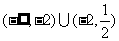 B.
B.
C.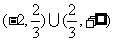 D.
D.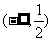
1.复数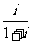 在复平面内的对应点到原点的距离为
( )
在复平面内的对应点到原点的距离为
( )
A.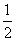 B.
B.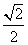 C.1 D.
C.1 D.
2.比较大小.

课堂小结:对数函数的图像与性质
作业:习题3-5A组3,4,5,6
1.求下列函数的定义域:
(1)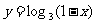 (2)
(2)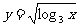 (3)
(3)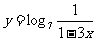 (4)
(4)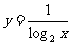
2.练习:画出下列函数的图像
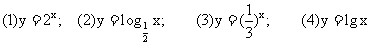
填表:对数函数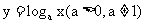 分别就其底数
分别就其底数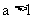 和
和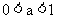 这两种情况的图像和性质:
这两种情况的图像和性质:
|
函 数 |
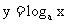 (a>1) (a>1) |
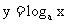 (0<a<1) (0<a<1) |
|
图 像 |
|
|
|
定义域 |
|
|
|
值 域 |
|
|
|
单调性 |
|
|
|
过定点 |
|
|
|
取值范围 |
|
|
例4.求下列函数的定义域:
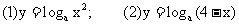
练习1:求下列函数的定义域
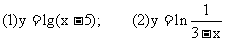
例5.比较下列各题中两个数的大小:
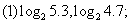

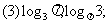
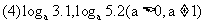
练习2:比较下列各组数中两个值的大小:
(1)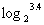 ,
,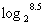 (2)
(2)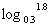 ,
,
(3)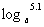 ,
,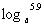 (a>0,且a≠1)
(a>0,且a≠1)
课堂补充练习:
3、情感.态度与价值观
通过学习对数函数,了解指数函数与对数函数图像和性质之间的关系.在学习的过程中体会类比、转化、数形结合的方法研究问题.直观明了,增强学习对数函数的积极性和自信心.
[学习重点]: 对数函数的图像和性质以及与指数函数图像与性质之间的关系.
[学习难点]:对数函数图像与性质与指数函数的图像与性质之间的关系.
[课时安排]: 2课时
[学习方法]:思考、探究.
[学习过程]
[新课导入]
[互动过程1]
复习:1.对数函数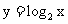 的图像与性质,以及与指数函数
的图像与性质,以及与指数函数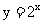 的图像与性质之间的关系
的图像与性质之间的关系
2、 过程与方法 
(1)掌握指数函数的图像与对数函数的图像之间的关系,会利用它们的对称关系,熟练地
进行画图.
(2)学会类比研究问题,利用数性结合的思想研究函数的性质.
1、知识与技能
(1)由前面学习指数函数的图像和对数函数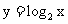 的图像的基础上,画出一般的对数函数的图像.
的图像的基础上,画出一般的对数函数的图像.
(2)会利用指数函数对数函数的图像研究对数函数的性质.
(3)能够理解指数函数的图像和性质与对数函数的图像与性质之间的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com