
课堂练习一
1、空气中按体积计算,含量最多的气体是 ( )
(A)氧气 (B)氮气 (C)二氧化碳 (D)稀有气体
当桌上有一个空烧杯时,小强同学说:“烧杯中什么都没有”;而小亮同学
却说:“烧杯中有物质”。你认为哪位同学说得对,理由是什么?;能用实验证明吗?
22.(13分)某地区的一特色水果上市时间能持续5个月。预测上市初期和后期会因供不应求呈连续上涨态势。而中期又将出现供大于求使价格下跌。现有三种模拟函数:
①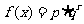 ②
②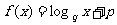 ③
③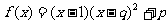
(p、q都为正常数且q>2)
(1)为准确研究其走势。应选哪种价格模拟函数,为什么?
(2)若f(1)=4,f(3)=6求所选函数f(x)的解析式(其中,定义域为[1,6],x=1表示4月1日,x=2表示5月1日,…,依次类推)。并求价格的活动范围,指出价格最低的月份。
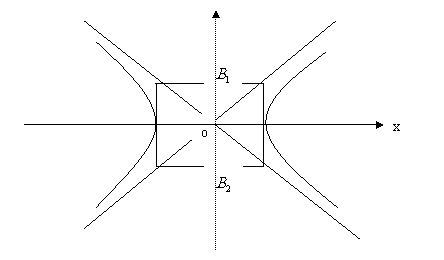
21.(13分)已知双曲线C的方程记为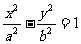 (a>0,b>0),点P(
(a>0,b>0),点P(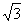 ,0)在双曲线上。离心率为e=2.
,0)在双曲线上。离心率为e=2.
(1)求双曲线方程;
(2)设双曲线C的虚轴的上、下端点分别为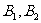 (如图)
(如图)
点A、B在双曲线上,且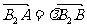
当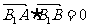 时,求直线AB的方程。
时,求直线AB的方程。
|

20.(12分)甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子;乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子。
(1)若甲在自己的箱子里任意取球,取后不放回。每次只取一个球,直到取出红球为止,求甲取球的次数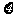 的数学期望。
的数学期望。
(2)若甲、乙两人各自从自己的箱子里任取一球比颜色,规定同色时为甲胜,异色时为乙胜。这种游戏规则公平吗?请说明理由。
19.(12分)在正方体ABCD-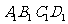 中,E、F分别为
中,E、F分别为
棱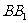 和
和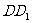 的中点,M为棱DC的中点。
的中点,M为棱DC的中点。
(1)求证平面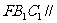 平面ADE
平面ADE
(2)求证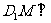 平面ADE
平面ADE
(3)求二面角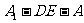 的余弦值
的余弦值
18.(12分)已知等差数列{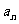 }的前n项和为
}的前n项和为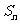
且 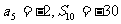
(1)
求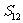
(2)
若数列{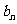 }满足
}满足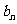 =
=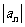 且{
且{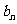 }前n项和为
}前n项和为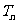 ,求
,求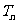
17.(12分)已知函数f(x)=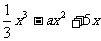
(1)a=3时,求f(x)的单调递减区间
(2)若f(x)在R上位增函数,求实数a的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com