
6.数列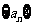 中,已知
中,已知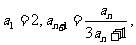 依次计算
依次计算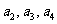 可猜得
可猜得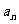 的表达式为(B)
的表达式为(B)
A.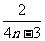 B.
B.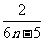 C.
C.
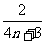 D.
D.
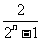
5.利用数学归纳法证明不等式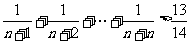 时,由
时,由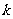 递推到
递推到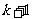 时,左边应添加的因式为(C)
时,左边应添加的因式为(C)
A.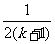 B.
B.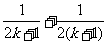 C.
C.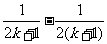 D.
D.
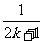
4.小明连续投篮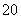 次,他的投篮命中率为
次,他的投篮命中率为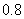 ,若
,若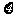 为投篮命中次数,则
为投篮命中次数,则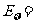 (A)
(A)
A.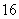 B.
B.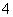 C.
C.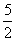 D.
D.
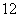
3.已知等比数列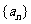 的前
的前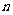 项和为
项和为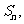 且
且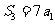 ,则数列
,则数列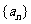 的公比
的公比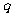 的值为(C)
的值为(C)
A.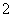 B.
B.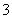 C.
C.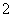 或
或 D.
D.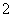 或
或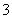
2.若书架中放有中文书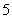 本,英文书
本,英文书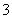 本,日文书
本,日文书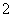 本,则抽出一本书为外文书的概率为(D)
本,则抽出一本书为外文书的概率为(D)
A.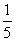 B.
B.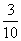 C.
C.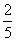 D.
D.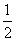
中,只有一项是符合题目要求的.(将答案涂在答题卡上)
1.从集合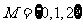 到集合
到集合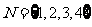 的不同映射的个数是(B)
的不同映射的个数是(B)
A.81个 B.64个 C.24个 D.12个
22. (本小题满分12分)
已知数列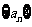 中,
中,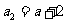 (
(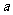 为常数),
为常数),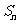 为
为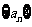 的前
的前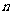 项和,且
项和,且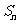 是
是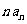 与
与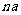 的等差中项.
的等差中项.
(Ⅰ)求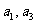 并归纳出
并归纳出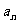 (不用证明);
(不用证明);
(Ⅱ)若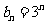 且
且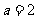 ,求数列
,求数列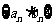 的前
的前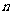 项和
项和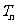 .
.
解:(1)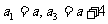 ,
,

(3)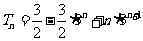
21.(本小题满分12分)
用黄、蓝、白三种颜色粉刷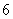 间办公室
间办公室
(Ⅰ) 若每间办公室刷什么颜色不要求,有多少种不同的粉刷方法?
(Ⅱ)若一种颜色粉刷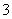 间,一种颜色粉刷
间,一种颜色粉刷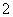 间,一种颜色粉刷
间,一种颜色粉刷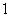 间,有多少种不同的粉刷方法?
间,有多少种不同的粉刷方法?
(Ⅲ)若每种颜色至少用一次,粉刷这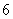 间办公室,有多少种不同的粉刷方法?
间办公室,有多少种不同的粉刷方法?
解:(1)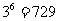 ;(2)
;(2)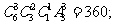
(3)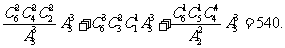
20. (本小题满分12分)
在数列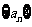 中,已知
中,已知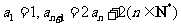
(Ⅰ)求证:数列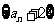 是等比数列;
是等比数列;
(Ⅱ) 求数列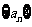 的前
的前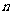 项和
项和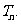
(1)略;(2)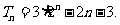
19. (本小题满分12分)
数列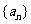 是首项
是首项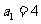 的等比数列,且
的等比数列,且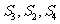 成等差数列.
成等差数列.
(Ⅰ)求数列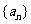 的通项公式;
的通项公式;
(Ⅱ)设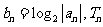 为数列
为数列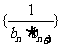 的前
的前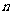 项和,求
项和,求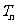 .
.
解 (I)当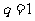 时,
时,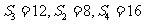 ,不成等差数列
,不成等差数列
当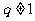 时,
时,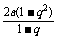 =
=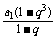 +
+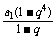
得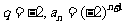
(II)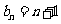 ,
,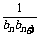 =
=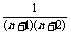 =
=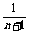 -
-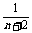
∴ +
+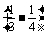 +…+
+…+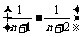 =
=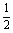 -
-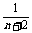 =
=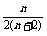
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com