1. 设0<x<1，则a=2，b=1+x， c=中最大的一个是　 ▲　 .

070]解：(1)6．(2)8．·················································································· (3分)

(3)①当0时，

． ··································· (5分)

②当3时，

=·································································································· (7分)

③当时，设与交于点．

(解法一)

过作则为等边三角形．

．

．··············································································· (10分)

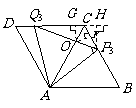
(解法二)

如右图，过点作于点，，于点

过点作交延长线于点．

又

又

·················································································· (10分)

069]解　 (1)易求得点的坐标为

由题设可知是方程即 的两根，

所以，所·························· (1分)

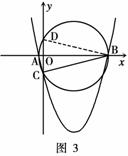
如图3，∵⊙P与轴的另一个交点为D，由于AB、CD是⊙P的两条相交弦，设它们的交点为点O，连结DB，∴△AOC∽△DOC，则······· (2分)

由题意知点在轴的负半轴上，从而点D在轴的正半轴上，

所以点D的坐标为(0，1)············································································ (3分)

(2)因为AB⊥CD， AB又恰好为⊙P的直径，则C、D关于点O对称，

所以点的坐标为，即···························································· (4分)

又，

所以解得······················ (6分)

067](1)解：∵直角梯形

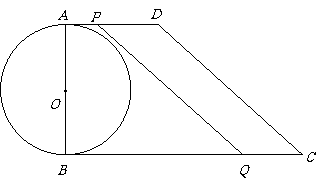
当时，四边形

为平行四边形．

由题意可知：

当时，四边形为平行四边形．································································· 3分

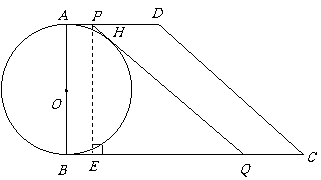(2)解：设与相切于点

过点作垂足为

直角梯形

由题意可知：

为的直径，

为的切线

····················································· 5分

在中，_，

即：_，，

_，因为在边运动的时间为秒

而_，(舍去)，当秒时，与相切．································ 8分

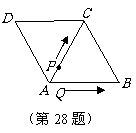
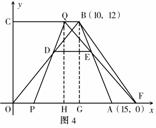[068]解：(1)如图4，过B作

则

过Q作

则

························································································· (2分)

要使四边形PABQ是等腰梯形，则，

即

或(此时是平行四边形，不合题意，舍去)························· (3分)

(2)当时，。

··············································· (4分)

···················································· (5分)

··································································· (6分)

(3)①当时，则

···························································································· (7分)

②当时，

即······················································ (8分)

③当时， ········· (9分)

综上，当时，△PQF是等腰三角形．·············· (10分)

066](1)由得，代入反比例函数中，得

∴反比例函数解析式为：··············································································· 2分

解方程组由化简得：

_，所以·································································· 5分

　 (2)无论点在之间怎样滑动，与总能相似．因为两点纵坐标相等，所以轴．

又因为轴，所以为直角三角形．

同时也是直角三角形，

···························································································· 8分

(在理由中只要能说出轴，即可得分．)

065]解：(1)∵AB是⊙O的直径(已知)

　　　　　　　 ∴∠ACB＝90º(直径所对的圆周角是直角)

　　　　　　　 ∵∠ABC＝60º(已知)

　　　　　　　 ∴∠BAC＝180º－∠ACB－∠ABC＝ 30º(三角形的内角和等于180º)

　　　　　　　 ∴AB＝2BC＝4cm(直角三角形中，30º锐角所对的直角边等于斜边的一半)

　　　　　　　 即⊙O的直径为4cm．

(2)如图10(1)CD切⊙O于点C，连结OC，则OC＝OB＝1/2·AB＝2cm．

∴CD⊥CO(圆的切线垂直于经过切点的半径)

∴∠OCD＝90º(垂直的定义)　　　　 ∵∠BAC＝ 30º(已求)

∴∠COD＝2∠BAC＝ 60º　 ∴∠D＝180º－∠COD－∠OCD＝ 30º∴OD＝2OC＝4cm　　　　　 ∴BD＝OD－OB＝4－2＝2(cm)

　　　　　　　 ∴当BD长为2cm，CD与⊙O相切．

(3)根据题意得：

BE＝(4－2t)cm，BF＝tcm；

如图10(2)当EF⊥BC时，△BEF为直角三角形，此时△BEF∽△BAC

∴BE：BA＝BF：BC即：(4－2t)：4＝t：2解得：t＝1

如图10(3)当EF⊥BA时，△BEF为直角三角形，此时△BEF∽△BCA

∴BE：BC＝BF：BA即：(4－2t)：2＝t：4解得：t＝1.6

∴当t＝1s或t＝1.6s时，△BEF为直角三角形．

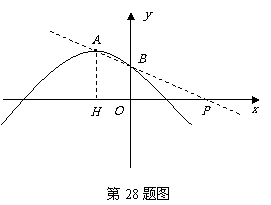
063](1)① 对称轴······································································ (2分)

② 当时，有_，解之，得 ，

∴ 点A的坐标为(，0)．·································································· (4分)

(2)满足条件的点P有3个，分别为(，3)，(2，3)，(，)．······· (7分)

(3)存在．当时，　 ∴ 点C的坐标为(0，3)

∵ DE∥轴，AO3，EO2，AE1，CO3

∴ ∽　 ∴ 　　即 　∴ DE1··········· (9分)

∴ 4

在OE上找点F，使OF，此时2，直线CF把四边形DEOC

分成面积相等的两部分，交抛物线于点M．························································ (10分)

设直线CM的解析式为，它经过点．则 · (11分)

解之，得 　　∴ 直线CM的解析式为 ·························· (12分)

[064]解：(1)抛物线与y轴的交于点B，令x=0得y=2．

∴B(0，2)　

∵ ∴A(-2，3)

(2)当点P是 AB的延长线与x轴交点时，

．

当点P在x轴上又异于AB的延长线与x轴的交点时，

在点P、A、B构成的三角形中，．

综合上述：

(3)作直线AB交x轴于点P，由(2)可知：当PA-PB最大时，点P是所求的点 ····· 8分

作AH⊥OP于H．∵BO⊥OP，∴△BOP∽△AHP

　　 ∴　 由(1)可知：AH=3、OH=2、OB=2，∴OP=4，故P(4，0)　

062]解：实践应用(1)2；．；．(2)．

拓展联想(1)∵△ABC的周长为l，∴⊙O在三边上自转了周．

又∵三角形的外角和是360°，

∴在三个顶点处，⊙O自转了(周)．　　　　　　　　　　　　　　　　　　　　　　　　　

∴⊙O共自转了(+1)周．

(2)+1．

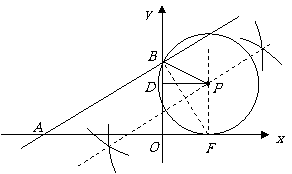
061]解(1)A(，0)，B(0，3)········································ 2分(每对一个给1分)

(2)满分3分．其中过F作出垂线1分，作出BF中垂线1分，找出圆心并画出⊙P给1分．　　 (注：画垂线PF不用尺规作图的不扣分)

(3)过点P作PD⊥轴于D，则PD=，BD=，··········· 6分

PB=PF=，∵△BDP为直角三形，∴

∴_，即

即∴与的函数关系为

(4)存在

解法1：∵⊙P与轴相切于点F，且与直线相切于点B

∴_，∵_，∴

∵AF=　 ，　 ∴_，∴ 11分

把代入，得

∴点P的坐标为(1，)或(9，15)12分

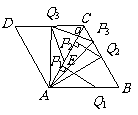
070]如图所示，菱形的边长为6厘米，．从初始时刻开始，点、同时从点出发，点以1厘米/秒的速度沿的方向运动，点以2厘米/秒的速度沿的方向运动，当点运动到点时，、两点同时停止运动，设、运动的时间为秒时，与重叠部分的面积为平方厘米(这里规定：点和线段是面积为的三角形)，解答下列问题：

(1)点、从出发到相遇所用时间是　　　　 秒；

(2)点、从开始运动到停止的过程中，当是等边三角形时的值是　　　　 秒；

(3)求与之间的函数关系式．