
2.正整数指数函数→整数指数函数→有理数指数函数
[互动过程3]
请同学们探讨一下整数指数幂的运算性质对于有理指数幂是否适用?
结论:整数指数幂的运算性质对于有理指数幂同样适用,即有以下运算性质:
(1).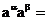
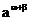 (2).
(2).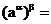
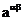 (3).
(3).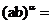
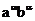
其中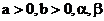 为有理数.
为有理数.
例5.求值:(1)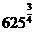 ;(2)
;(2)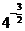 ;(3)
;(3)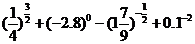
解:(1)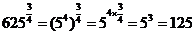 ;
;
(2)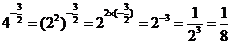 ;
;
(3)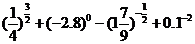
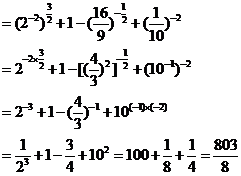
例6.计算下列各式(式子中字母都是正数),并把结果化为只含正有理指数的形式:
(1)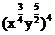 ;(2)
;(2)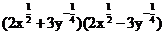
解:(1)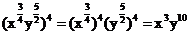 ;
;
(2)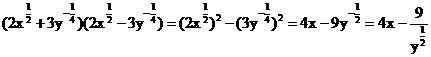
练习: 3,4
小结:
1.正整数指数幂→负分数指数幂→整数指数幂→正分数指数幂→负分数指数幂→分数指数幂
2.正分数指数幂:
一般地,给定正实数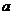 ,对于任意给定的正整数
,对于任意给定的正整数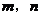 ,存在唯一的正实数
,存在唯一的正实数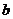 ,使得
,使得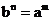 ,我们把
,我们把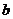 叫做
叫做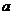 的
的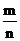 次幂,记作
次幂,记作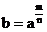 ,它就是正分数指数幂.
,它就是正分数指数幂.
例如: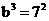 ,则
,则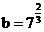 ;
;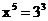 ,则
,则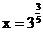 等.
等.
说明: 有时我们把正分数指数幂写成根式的形式,即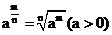 ,例如:
,例如: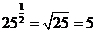 ;
;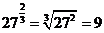
例1.把下列各式中的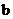 写成正分数指数幂的形式:
写成正分数指数幂的形式:
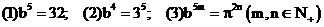
解:(1)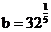 ;(2)
;(2)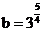 ;(3)
;(3)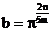
练习1:把下列各式中的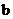 写成正分数指数幂的形式:
写成正分数指数幂的形式:
(1)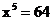 ;(2)
;(2)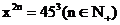
例2:计算:(1)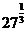 ;(2)
;(2)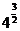
解:(1)因为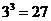 ,所以
,所以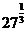 =3;
=3;
(2)因为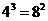 ,所以
,所以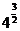 =8
=8
练习:计算(1)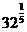 ;(2)
;(2)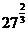
[互动过程2]
请同学们回顾负整数指数幂的定义,能否类似地引入负分数指数幂呢?
正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定
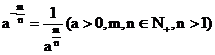 ;
;
说明:(1).0的正分数指数幂等于0,0的负分数指数幂没有意义.
(2)规定了分数指数幂的意义后,指数的概念就从整数推广到有理指数.当我们把正整数指数幂推广到有理指数幂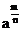 或
或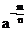
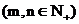 时,对底数
时,对底数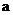 应有所限制,即
应有所限制,即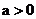 .
.
(3)对于每一个有理数我们都定义了一个有理指数与它对应,这样就可以把整数指数函数扩展到有理指数函数,一个定义在有理数集上的指数函数.
例3.把下列各式中的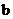 写为负分数指数幂的形式:
写为负分数指数幂的形式:
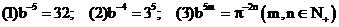
解:(1)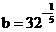 ;(2)
;(2)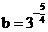 ;(3)
;(3)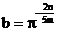
例4.计算:(1)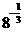 ;(2)
;(2)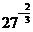
解:(1)因为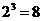 ,所以
,所以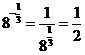
(2)因为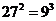 ,所以
,所以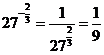 .
.
练习: 1,2,
前面我们已经把正整数指数幂扩充到整数指数幂,还要进一步扩充到分数指数幂.有许多问题都不是整数指数.例如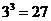 ,若已知
,若已知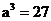 ,你能表示出
,你能表示出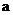 吗?怎样表示?我们引入分数指数幂表示为
吗?怎样表示?我们引入分数指数幂表示为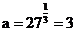 .
.
1.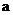 的
的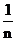 次幂:
次幂:
一般地,给定正实数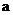 ,对于给定的正整数
,对于给定的正整数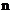 ,存在唯一的正实数
,存在唯一的正实数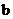 ,使得
,使得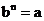 ,我们把
,我们把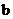 叫做
叫做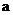 的
的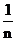 次幂,记作
次幂,记作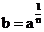 .
.
例如: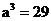 ,则
,则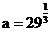 ;
;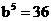 ,则
,则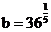 .
.
由于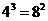 ,我们也可以记作
,我们也可以记作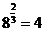

26.(12分)如图所示有一种自动夹具,两条铁臂能绕转轴O自由转动,它能夹紧重物将其提升起来。每条铁臂粗细、质量均匀,长为1.2m,重为200N。
(1)现该自动夹具夹起一个宽为0.8m、重为40N的重物时,一侧铁臂对重物的压力为多大?
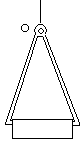 (2)若铁臂对重物的静摩擦力最多为压力的0.5倍,则要吊起重为40N的重物,对重物宽度有何限制?
(2)若铁臂对重物的静摩擦力最多为压力的0.5倍,则要吊起重为40N的重物,对重物宽度有何限制?
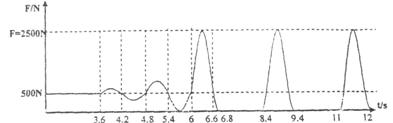
25、(14分)一位蹦床运动员仅在竖直方向上运动,弹簧床对运动员的弹力F随时间t的变化规律通过传感器用计算机绘制出来,如图所示。结合图像, 试求:
(1)运动员的质量;
(2)运动过程中,运动员最大加速度;
(3)不计空气阻力,运动过程中,运动员离开蹦床上升的最大高度
24、(12分)据报道,一儿童玩耍时不慎从36m高的阳台上无初速掉下,在他刚掉下时恰被楼下社区管理人员发现,该人员迅速由静止冲向儿童下落处的正下方楼底,准备接住儿童。已知管理人员到楼底的距离为18m,为确保能稳妥安全接住儿童,管理人员将尽力节约时间,但又必须保证接儿童时没有水平方向的冲击(即水平速度为零)。设儿童下落过程中所受空气阻力约为儿童本身重力的0.2倍,将儿童和管理人员都看作质点,g取10m/s2。
(1)管理人员至少用多大的平均速度跑到楼底?
(2)若管理人员在奔跑过程中做匀加速或匀减速运动的加速度大小相等,且最大速度不超过9m/s,求管理人员奔跑时加速度的大小需满足什么条件?
23.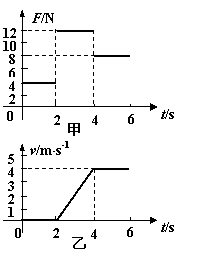 (12分)一物块在粗糙水平面上,受到的水平拉力F随时间t变化如图甲所示,速度v随时间t变化如图乙所示(g=10m/s2)。求:
(12分)一物块在粗糙水平面上,受到的水平拉力F随时间t变化如图甲所示,速度v随时间t变化如图乙所示(g=10m/s2)。求:
(1)1秒末物块所受摩擦力f的大小。
(2)物块的质量m。
(3)物块与水平面间的动摩擦因数m。
22.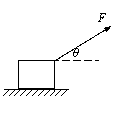 辨析题:(10分)如图所示,木块质量m=0.78kg,在与水平方向成37°角、斜向右上方的恒定拉力F作用下,以a=2.0m/s2的加速度从静止开始做匀加速直线运动,在3s末时撤去拉力F。已知木块与地面间的动摩擦因数m=0.4,(sin37°=0.60,cos37°=0.80。)求:拉力F的大小以及物体在5s内滑行的总位移。
辨析题:(10分)如图所示,木块质量m=0.78kg,在与水平方向成37°角、斜向右上方的恒定拉力F作用下,以a=2.0m/s2的加速度从静止开始做匀加速直线运动,在3s末时撤去拉力F。已知木块与地面间的动摩擦因数m=0.4,(sin37°=0.60,cos37°=0.80。)求:拉力F的大小以及物体在5s内滑行的总位移。
某同学是这样分析的:由牛顿第二定律可得Fcosq-mmg=ma,可求出拉力F的大小。物体加速阶段滑行的时间t1=3s,位移s1=at12,末速度v1=at1,减速阶段滑行的时间t2=2s,加速度a'=mg,可求出位移s2,则滑行的总位移s=s1+s2。你认为这位同学的分析是否正确,若正确,请列式并完成计算;若不正确,请说明理由,并用你自己的方法算出正确的结果。
21、如下图甲所示是用手握住钢钳夹住一长方体工件时的情景。为了研究钢钳的平衡情况,可将钢钳抽象为两个杠杆模型,其中一个如图乙中实线所示,今在A点施加一个大小不变、方向始终垂直于AB的握力F,则在下列情况发生时,其中判断正确的是----------------------------( )
(A)将工件往右抽动时比往左抽动时容易
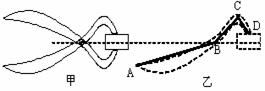 (B)将工件往左抽动时比往右抽动时容易
(B)将工件往左抽动时比往右抽动时容易
(C)向右抽动时,将工件横置(夹住部分较薄)容易抽动
(D)向右抽动时,将工件竖置(夹住部分较厚)容易抽动
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com