
4.下列句子中没有语病且句意明确的一项是 ( )
A.得罪了老张的业务主管,事后懊悔不已,他总想找机会向对方道个歉、解释清楚,以便消除误会。
B.天津市援建陕西省强县“农家书屋”,目的是送知识、送信息到灾区;这一举措一开始就特别引起当地广大农民的关注。
C.2010年世博会之所以在上海举行,是由于这座城市发展的大环境所决定的,因此,中小企业要在世博会中大展拳脚,就得看清门前的市场环境。
D.作为一种道德标准,“八荣八耻”积淀着中华民族传统的道德内涵,也折射出中华民族新时期的道德追求,我们能否将我国建设成文明的社会主义强国将直接取决于对这一标准的落实。
3.下列各句横线处应填入的词语,最恰当的一组是 ( )
①云南有着美丽的风景,山清水秀,月色朦胧;风摇叶展,山路 ;九转十八盘,山雨
雾中行。
②“耶路撒冷”是和平之城的意思,却又是遭受劫难最多的城市,可是长期的冲突并没有使其失去迷人的魅力, 使旅游者望而却步。
③互联网并非_______、整齐划一的技术革命的产物,而是在各种混乱、争论和复杂的利益纠葛中发展成今天的规模。正是一个个小的草根网络,最终汇集成一个不可逆转的大潮流。
A.曼延 进而 自上而下 B.蔓延 从而 一呼百应
C.曼延 进而 一呼百应 D.蔓延 从而 自上而下
2.下列词语中没有错别字的一组是 ( )
A.蕴育 清彻 乔装打扮 九层之台,起于垒土
B.委曲 喟叹 冒然行事 明枪易躲,暗箭难防
C.平添 度假 坚如磐石 言者无罪,闻者足诫
D.简练 装潢 相辅相成 黄钟毁弃,瓦釜雷鸣
1.下列词语中加点的字的读音,全都正确的一组是 ( )
A.因为(wéi) 付梓(zǐ) 膀(pāng)肿 窗明几(jī)净
B.祈(qí)祷 褫(chǐ)夺 轧(yà)钢 逸兴遄(chuán)飞
C.锁钥(yuè) 伧(cāng)俗 监(jiàn)生 骈(pián)拇枝指
D.翘(qiáo)首 铜臭(xiù) 叱咤(zhà) 薄(báo)利多销
16.已知 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,且在
,且在 内,关于
内,关于 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是 
三 解答题
17记关于 的不等式
的不等式 的解集为
的解集为 ,不等式
,不等式 的解集为
的解集为 .
.
(1)若 ,求
,求 ;
;
(2)若 ,求正数
,求正数 的取值范围
的取值范围
17解:(1)由 ,得
,得 .
.
(2) .
.
由 ,得
,得 ,又
,又 ,所以
,所以 ,
,
即 的取值范围是
的取值范围是 .
.
18设p:实数x满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(Ⅰ)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若 是
是
 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
18解:由 得
得 ,
,
又 ,所以
,所以 ,
,
当 时,1<
时,1< ,即
,即 为真时实数
为真时实数 的取值范围是1<
的取值范围是1< .
.
由 ,得
,得 ,即
,即 为真时实数
为真时实数 的取值范围是
的取值范围是 .
.
若 为真,则
为真,则 真且
真且 真,
真,
所以实数 的取值范围是
的取值范围是 .
.
(Ⅱ)  是
是 的充分不必要条件,即
的充分不必要条件,即

 ,且
,且

 ,
,
设A= ,B=
,B= ,则
,则
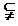
 ,
,
又A= =
= ,
B=
,
B= =
= },
},
则0< ,且
,且
所以实数 的取值范围是
的取值范围是 .
.
19两个二次函数 与
与 的图象有唯一的公共点
的图象有唯一的公共点 ,
,
(1)求 的值;
的值;
(2)设 ,若
,若 在
在 上是单调函数,求
上是单调函数,求 的范围,并指出是单调递增函数,还是单调递减函数。
的范围,并指出是单调递增函数,还是单调递减函数。
19解:(1)由已知得
 化简得
化简得

且
即 有唯一解
有唯一解
所以
即 
消去 得
得
 ,
,
解得
(2)


若 在
在 上为单调函数,则
上为单调函数,则 在
在 上恒有
上恒有 或
或 成立。
成立。
因为 的图象是开口向下的抛物线,
的图象是开口向下的抛物线,
所以 时
时 在
在 上为减函数,
上为减函数,
所以 ,解得
,解得

即 时,
时, 在
在 上为减函数。
上为减函数。
20已知函数 .
.
(1)求 在[0,1]上的单调区间;
在[0,1]上的单调区间;
(2)若对任意 ,不等式
,不等式 ,求实数a的取值范围.
,求实数a的取值范围.
20解(1)函数f(x)的定义域为 ,
,

∴在[0,1]上,当 时,
时, 单调递增;
单调递增;
当 时,
时, ,
, 单调递减.
单调递减.
∴ 在[0,1]上的增区间是
在[0,1]上的增区间是 ,减区间是
,减区间是 .(开闭均可)
.(开闭均可)
(2)由 ,可得
,可得 或
或 ,
,
即 或
或 .
.
由(1)当 时,
时, ,
,
 .
.
∵ 恒成立,∴
恒成立,∴ ,
,
∵ 恒成立,∴
恒成立,∴ .
.
 的取值范围为:
的取值范围为:
21已知函数 的导函数为
的导函数为 ,
, 。
。
⑴当 时,求函数
时,求函数 的单调区间;
的单调区间;
⑵若对满足 的一切
的一切 的值,都有
的值,都有 ,求实数
,求实数 的取值范围;
的取值范围;
⑶若 对一切
对一切 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
21解:⑴当 时,
时, 。令
。令 得
得 ,故当
,故当 时
时 ,
, 单调递增;当
单调递增;当 时
时 ,
, 单调递减。所以函数
单调递减。所以函数 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;
⑵法一:因 ,故
,故 。
。
令 ,要使
,要使 对满足
对满足 的一切
的一切 成立,
成立,
则 ,解得
,解得 ;
;
法二: ,故
,故 。由
。由 可解得
可解得
 。因为
。因为 在
在 单调递减,因此
单调递减,因此 在
在 单调递增,故
单调递增,故 。
。
设 ,则
,则 ,
,
因为 ,所以
,所以 ,从而
,从而 在
在 单调递减,
单调递减,
故 。因此
。因此 ,即
,即 。
。
⑶因为 ,所以
,所以 即
即 对一切
对一切 恒成立。
恒成立。 ,令
,令 ,则
,则 。因为
。因为 ,所以
,所以 ,故
,故 在
在 单调递增,有
单调递增,有 。因此
。因此 ,从而
,从而 。所以
。所以 。
。
22设函数 。
。
(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值;
(2)当x∈时[a+1,a+2],不等式 恒成立,求a的取值范围。
恒成立,求a的取值范围。
22解(1)∵f′(x)=-x2+4ax-3a2=-(x-3a)(x-a),由f′(x)>0得:a<x<3a
由f′(x)<0得,x<a或x>3a,
则函数f(x)的单调递增区间为(a,3a),单调递减区间为(-∞,a)和(3a,+∞)列表如下:
|
x |
(-∞,a) |
a |
(a, 3a) |
3a |
(3a,+ ∞) |
|
f′(x) |
- |
0 |
+ |
0 |
- |
|
f(x) |
↘ |
- a3+b a3+b |
↗ |
b |
↘ |
∴函数f(x)的极大值为b,极小值为- a3+b
a3+b
(2)
 上单调递减,
上单调递减,
因此
∵不等式|f′(x)|≤a恒成立,
即a的取值范围是
15.若函数 的值域为
的值域为 ,则实数
,则实数 的取值范围是_
的取值范围是_ ______。
______。
14.已知曲线 在
在 点处的切线与曲线
点处的切线与曲线 在
在 点处的切线互相平行,则
点处的切线互相平行,则 的值为 0或 -2/3
.
的值为 0或 -2/3
.
12.已知函数f(x)= ,则f(1-x)的图象是( D )
,则f(1-x)的图象是( D )
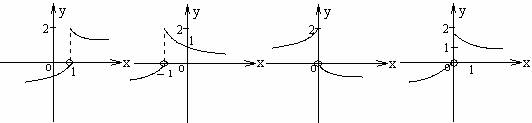
A B C D
二填空题
13已知集合 等于
等于 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com