
4.索契作为冬奥会举办地的优势条件是
A.冬季晴天多,阳光充足 B.冬季北部高山积雪量大
C.地理位置优越,交通便利 D.依山傍海,空气清新
下图中a为晨昏线,c为经线,b为C线上地球自转线速度最大的点,读图回答5-6题。
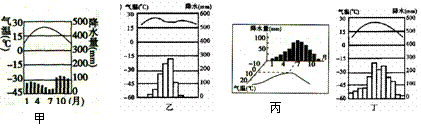
3.右面四幅图中能反映索契气候的是
A.甲 B.乙 C.丙 D.丁
2.a、b、c、d四小组所在坡地中,坡度最陡的是
A.a B. b C.c D.d
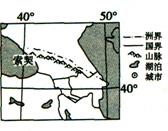 2010年2月28日温哥华冬奥会落下帷幕,2014年冬奥会计划于当年的2月7日至23日在俄罗斯南部城市索契举行。索契是世界三大夏都之一,读图回答3-4题。
2010年2月28日温哥华冬奥会落下帷幕,2014年冬奥会计划于当年的2月7日至23日在俄罗斯南部城市索契举行。索契是世界三大夏都之一,读图回答3-4题。
1.村庄所处的 局部地形是
局部地形是
A.山脊 B.山间盆地 C.鞍部 D.山顶
22. 设函数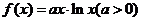 .
.
(Ⅰ)当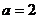 时,判断函数
时,判断函数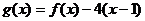 的零点的个数,并且说明理由;
的零点的个数,并且说明理由;
(Ⅱ)若对所有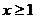 ,都有
,都有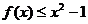 ,求正数
,求正数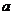 的取值范围.
的取值范围.
21. 如图,已知圆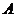 过定点
过定点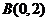 ,圆心
,圆心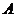 在抛物线
在抛物线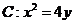 上运动,
上运动,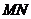 为圆
为圆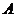 在
在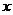 轴上所截得的弦.
轴上所截得的弦.
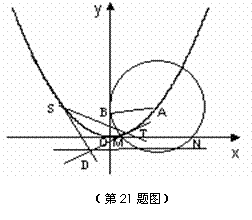 (Ⅰ)证明:
(Ⅰ)证明: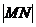 是定值;
是定值;
(Ⅱ)讨论抛物线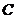 的准线
的准线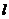 与圆
与圆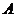 的位置关系;
的位置关系;
(Ⅲ)设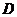 是抛物线
是抛物线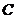 的准线
的准线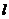 上任意一点,过
上任意一点,过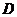 向抛物线作两条切线
向抛物线作两条切线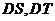 (切点是
(切点是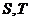 ),判断直线
),判断直线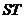 是否过定点,并证明你的结论.
是否过定点,并证明你的结论. 
20. 如图1,在直角梯形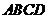 中,
中,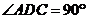 ,
,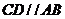 ,
,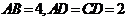 ,
, 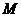 为线段
为线段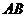 的中
的中 点.将
点.将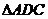 沿
沿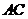 折起,使平面
折起,使平面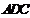
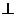 平面
平面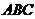 ,得到几何体
,得到几何体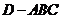 ,如图2所示.
,如图2所示.
(Ⅰ) 求证: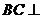 平面
平面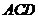 ;
;
 (Ⅱ) 求二面角
(Ⅱ) 求二面角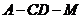 的余弦值.
的余弦值.
19. 在一个盒子中,放有标号分别为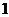 ,
, ,
,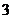 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为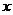 、
、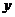 ,记
,记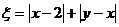 .
.
(Ⅰ)求随机变量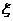 的最大值,并求事件“
的最大值,并求事件“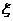 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量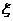 的分布列和数学期望.
的分布列和数学期望.
18.已知△ABC的顶点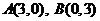 ,
,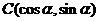 ,其中0<
,其中0<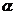 <
<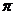 .
.
(Ⅰ)若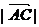 =
=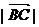 ,求角
,求角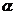 的值;
的值;
(Ⅱ)若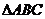 的面积为
的面积为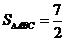 ,求
,求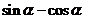 的值
的值
17. 设函数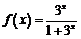 ,若
,若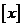 表示不大于
表示不大于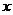 的最大整数,则函数
的最大整数,则函数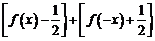 的值域是 ▲ .
的值域是 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com