
3. ⑴(理)依题意,甲答对试题数ξ的概率分布如下:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
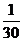 |
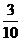 |
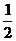 |
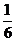 |
甲答对试题数ξ的数学期望Eξ=0×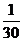 +1×
+1×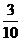 +2×
+2×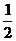 +3×
+3×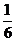 =
=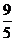 .
.
⑴(文)设甲、乙两人考试合格的事件分别为A、B,则
P(A)=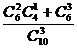 =
=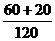 =
=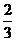 , P(B)=
, P(B)=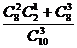 =
=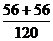 =
=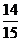 .
.
答:甲、乙两人考试合格的概率分别为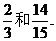
⑵解法一、因为事件A、B相互独立,所以甲、乙两人考试均不合格的概率为
P(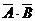 )=P(
)=P(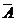 )P(
)P(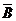 )=(1-
)=(1-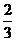 )(1-
)(1-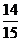 )=
)=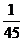 .
.
∴甲、乙两人至少有一人考试合格的概率为
P=1-P(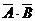 )=1-
)=1-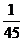 =
=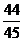 .
.
答:甲、乙两人至少有一人考试合格的概率为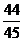 .
.
解法二:因为事件A、B相互独立,所以甲、乙两人至少有一人考试合格的概率为
P=P(A·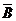 )+P(
)+P(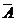 ·B)+P(A·B)=P(A)P(
·B)+P(A·B)=P(A)P(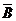 )+P(
)+P(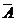 )P(B)+P(A)P(B)
)P(B)+P(A)P(B)
=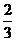 ×
×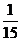 +
+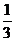 ×
×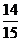 +
+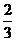 ×
×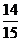 =
=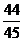 .
.
答:甲、乙两人至少有一人考试合格的概率为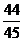 .
.
2. (1)y=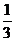 ,x=
,x=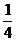 或y=
或y=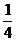 ,x=
,x=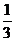 ;(2)
;(2)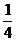
1. (Ⅰ)甲取1次乙取2次或甲取2次乙取1次,P =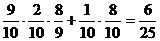 .
.
(Ⅱ)对立事件甲取2次乙取3次的概率为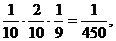 所求概率P=
所求概率P=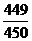 .
.
(Ⅲ)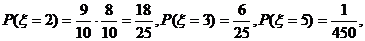
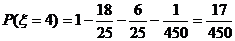 ,分布列为(略)
,分布列为(略)
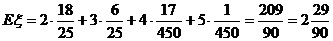 .
.
6. 某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求ξ的分布及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞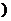 上单调递增”为事件A,求事件A的概率.
上单调递增”为事件A,求事件A的概率.
解答题答案:
5. A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为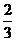 ,服用B有效的概率为
,服用B有效的概率为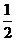 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)(理) 观察3个试验组,用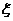 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求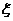 的分布列和数学期望。
的分布列和数学期望。
(文)观察3个试验组,求这3个试验组中至少有一个甲类组的概率。
4. 下表为某班英语及数学成绩的分布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为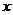 ,数学成绩为
,数学成绩为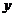 。设
。设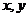 为随机变量(注:没有相同姓名的学生)。
为随机变量(注:没有相同姓名的学生)。
 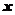 |
数学 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
英语 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
9 |
3 |
|
|
2 |
1 |
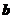 |
6 |
0 |
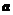 |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
(1)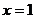 的概率为多少?
的概率为多少?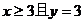 的概率为多少?
的概率为多少?
(2)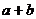 等于多少?若
等于多少?若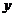 的期望为
的期望为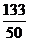 ,试确定
,试确定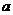 ,
,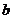 的值。
的值。
3. 甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
⑴(理)求甲答对试题数ξ的概率分布及数学期望;(文)分别求甲、乙两人考试合格的概率;
⑵求甲、乙两人至少有一人考试合格的概率.
2. 设A、B、C三个事件相互独立,事件A发生的概率是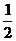 ,A、B、C中只有一个发生的概率是
,A、B、C中只有一个发生的概率是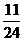 ,又A、B、C中只有一个不发生的概率是
,又A、B、C中只有一个不发生的概率是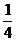 。
。
①求事件B发生的概率及事件C发生的概率;②试求A、B、C均不发生的概率。
1. 在甲袋中有10个螺母,其中9个正品,1个次品;乙袋中有10个螺帽,其中8个正品,2个次品.现要抽取1套正品螺栓(即正品螺母、正品螺帽各一),若随机不放回地进行抽取,先定螺母,后定螺帽.
(Ⅰ)求总共抽取的次数恰好为3的概率;
(Ⅱ)求总共抽取的次数不超过4概率;
(Ⅲ)(理科做)求总共抽取的次数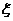 的分布列和数学期望.
的分布列和数学期望.
22、(本题满分14分)

 w_w w. k#s5_
w_w w. k#s5_
已知二次函数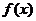 满足:①当
满足:①当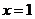 时有极值;2图像与
时有极值;2图像与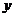 轴的交点的纵坐标为
轴的交点的纵坐标为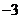 ,且在该点处的切线与直线
,且在该点处的切线与直线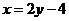 垂直。
垂直。
(1)求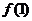 的值;
的值;
(2)求函数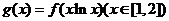 的值域;
的值域;
(3)若曲线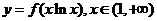 上任意一点处的切线的斜率恒大于
上任意一点处的切线的斜率恒大于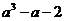 ,试求实数
,试求实数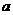 的取值范围。
的取值范围。


 w_w w. k#s5_
w_w w. k#s5_



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com