
014](1)解:∵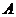 点第一次落在直线
点第一次落在直线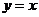 上时停止旋转,∴
上时停止旋转,∴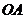 旋转了
旋转了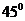 .
.
∴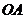 在旋转过程中所扫过的面积为
在旋转过程中所扫过的面积为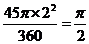 .……………4分
.……………4分
(2)解:∵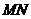 ∥
∥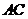 ,∴
,∴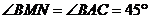 ,
,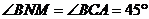 .
.
∴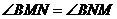 .∴
.∴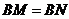 .又∵
.又∵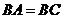 ,∴
,∴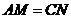 .
.
又∵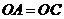 ,
,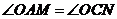 ,∴
,∴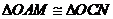 .∴
.∴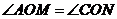 .∴
.∴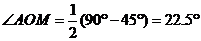 .∴旋转过程中,当
.∴旋转过程中,当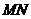 和
和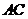 平行时,正方形
平行时,正方形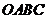 旋转的度数为
旋转的度数为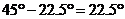 .……………………………………………8分
.……………………………………………8分
(3)答: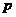 值无变化. 证明:延长
值无变化. 证明:延长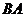 交
交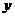 轴于
轴于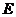 点,则
点,则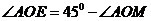 ,
,
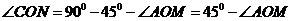 ,∴
,∴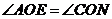 .又∵
.又∵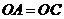 ,
,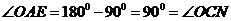 .∴
.∴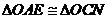 .∴
.∴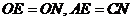 .
.
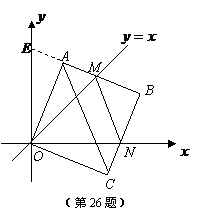 又∵
又∵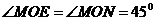 ,
, , ∴
, ∴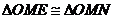 .
.
∴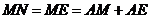 .∴
.∴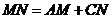 ,
,
∴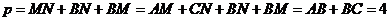 .
.
∴在旋转正方形 的过程中,
的过程中,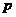 值无变化. ……………12分
值无变化. ……………12分
013]解:(1)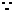 该抛物线过点
该抛物线过点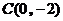 ,
, 可设该抛物线的解析式为
可设该抛物线的解析式为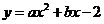 .
.
将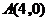 ,
,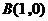 代入,
代入,
得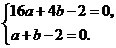 解得
解得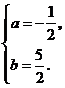
 此抛物线的解析式为
此抛物线的解析式为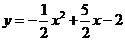 .························································ (3分)
.························································ (3分)
(2)存在.··········································································································· (4分)
如图,设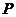 点的横坐标为
点的横坐标为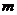 ,
,
 则
则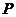 点的纵坐标为
点的纵坐标为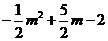 ,
,
当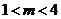 时,
时,
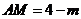 ,
,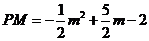 .
.
又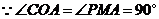 ,
,
 ①当
①当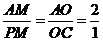 时,
时,
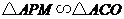 ,
,
即 .
.
解得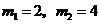 (舍去),
(舍去),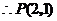 .····························································· (6分)
.····························································· (6分)
②当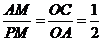 时,
时,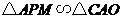 ,即
,即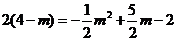 .
.
解得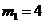 ,
,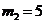 (均不合题意,舍去)
(均不合题意,舍去)
 当
当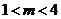 时,
时,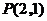 .················································································· (7分)
.················································································· (7分)
类似地可求出当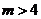 时,
时,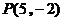 .································································· (8分)
.································································· (8分)
当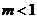 时,
时,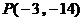 .
.
综上所述,符合条件的点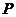 为
为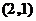 或
或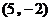 或
或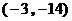 .······························ (9分)
.······························ (9分)
(3)如图,设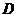 点的横坐标为
点的横坐标为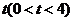 ,则
,则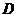 点的纵坐标为
点的纵坐标为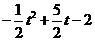 .
.
过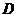 作
作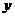 轴的平行线交
轴的平行线交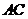 于
于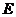 .由题意可求得直线
.由题意可求得直线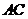 的解析式为
的解析式为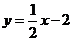 . (10分)
. (10分)
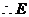 点的坐标为
点的坐标为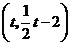 .
.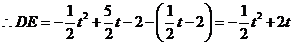 .·· (11分)
.·· (11分)
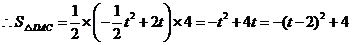 .
.
 当
当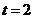 时,
时, 面积最大.
面积最大.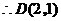 .···················································· (13分)
.···················································· (13分)
012]解:(1)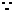 圆心
圆心 在坐标原点,圆
在坐标原点,圆 的半径为1,
的半径为1,
 点
点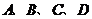 的坐标分别为
的坐标分别为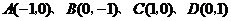
 抛物线与直线
抛物线与直线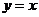 交于点
交于点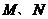 ,且
,且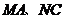 分别与圆
分别与圆 相切于点
相切于点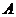 和点
和点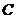 ,
,

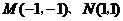 .
. 点
点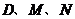 在抛物线上,将
在抛物线上,将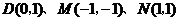 的坐标代入
的坐标代入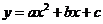 ,得:
,得: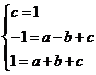 解之,得:
解之,得: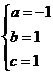
 抛物线的解析式为:
抛物线的解析式为: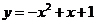 .······································································ 4分
.······································································ 4分
(2)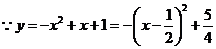
 抛物线的对称轴为
抛物线的对称轴为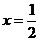 ,
,
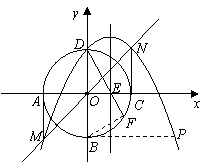
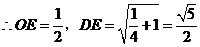 .···················· 6分
.···················· 6分
连结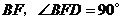 ,
,
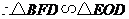 ,
,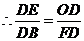 ,
,
又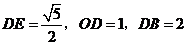 ,
,
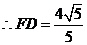 ,
,
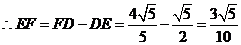 .····································································· 8分
.····································································· 8分
(3)点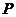 在抛物线上.································································································ 9分
在抛物线上.································································································ 9分
设过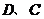 点的直线为:
点的直线为: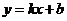 ,
,
将点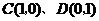 的坐标代入
的坐标代入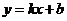 ,得:
,得: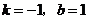 ,
,
 直线
直线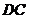 为:
为: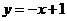 .······················································································ 10分
.······················································································ 10分
过点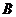 作圆
作圆 的切线
的切线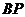 与
与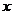 轴平行,
轴平行,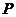 点的纵坐标为
点的纵坐标为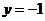 ,
,
将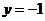 代入
代入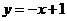 ,得:
,得: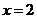 .
.

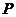 点的坐标为
点的坐标为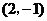 ,当
,当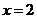 时,
时,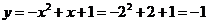 ,
,
所以,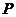 点在抛物线
点在抛物线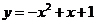 上.···································································· 12分
上.···································································· 12分
011]解:(1)证明:在Rt△FCD中,∵G为DF的中点,∴ CG= FD.………1分
同理,在Rt△DEF中,EG= FD.…………2分∴ CG=EG.…………………3分
(2)(1)中结论仍然成立,即EG=CG.…………………………4分
证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.
在△DAG与△DCG中,∵ AD=CD,∠ADG=∠CDG,DG=DG,
∴ △DAG≌△DCG.∴ AG=CG.………………………5分
在△DMG与△FNG中,∵ ∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴ △DMG≌△FNG.∴ MG=NG 在矩形AENM中,AM=EN. ……………6分
在Rt△AMG 与Rt△ENG中,∵ AM=EN, MG=NG,
∴ △AMG≌△ENG.∴ AG=EG.∴ EG=CG. ……………………………8分
证法二:延长CG至M,使MG=CG,
连接MF,ME,EC, ……………………4分
在△DCG 与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,
∴△DCG ≌△FMG.∴MF=CD,∠FMG=∠DCG.
∴MF∥CD∥AB.………………………5分∴ 在Rt△MFE 与Rt△CBE中,
∵ MF=CB,EF=BE,∴△MFE ≌△CBE.∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°.∴ △MEC为直角三角形.∵ MG = CG,∴ EG= MC.………8分
(3)(1)中的结论仍然成立,即EG=CG.其他的结论还有:EG⊥CG.……10分
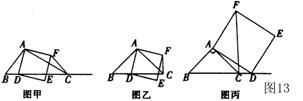
020]如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连结AD,以AD为一边且在AD的右侧作正方形ADEF。
解答下列问题:
(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 。
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90°点D在线段BC上运动。
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由。(画图不写作法)
(3)若AC=4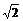 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值。
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值。
019]如图所示,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CF-EO|,再以CM、CO为边作矩形CMNO
(1)试比较EO、EC的大小,并说明理由
(2)令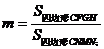 ,请问m是否为定值?若是,请求出m的值;若不是,请说明理由
,请问m是否为定值?若是,请求出m的值;若不是,请说明理由
(3)在(2)的条件下,若CO=1,CE=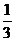 ,Q为AE上一点且QF=
,Q为AE上一点且QF=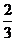 ,抛物线y=mx2+bx+c经过C、Q两点,请求出此抛物线的解析式.
,抛物线y=mx2+bx+c经过C、Q两点,请求出此抛物线的解析式.
(4)在(3)的条件下,若抛物线y=mx2+bx+c与线段AB交于点P,试问在直线BC上是否存在点K,使得以P、B、K为顶点的三角形与△AEF相似?若存在,请求直线KP与y轴的交点T的坐标?若不存在,请说明理由。
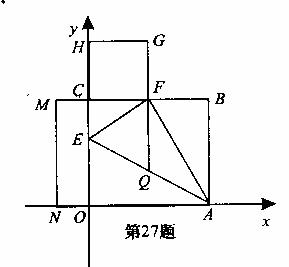
018]如图,抛物线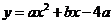 经过
经过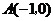 、
、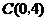 两点,与
两点,与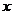 轴交于另一点
轴交于另一点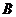 .
.
(1)求抛物线的解析式;
(2)已知点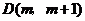 在第一象限的抛物线上,求点
在第一象限的抛物线上,求点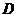 关于直线
关于直线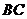 对称的点的坐标;
对称的点的坐标;
(3)在(2)的条件下,连接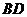 ,点
,点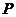 为抛物线上一点,且
为抛物线上一点,且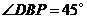 ,求点
,求点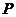 的坐标.
的坐标.
017]如图,已知抛物线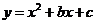 经过
经过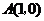 ,
,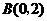 两点,顶点为
两点,顶点为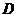 .
.
(1)求抛物线的解析式;
(2)将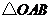 绕点
绕点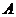 顺时针旋转90°后,点
顺时针旋转90°后,点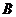 落到点
落到点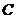 的位置,将抛物线沿
的位置,将抛物线沿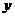 轴平移后经过点
轴平移后经过点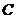 ,求平移后所得图象的函数关系式;
,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与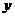 轴的交点为
轴的交点为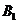 ,顶点为
,顶点为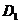 ,若点
,若点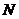 在平移后的抛物线上,且满足
在平移后的抛物线上,且满足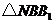 的面积是
的面积是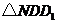 面积的2倍,求点
面积的2倍,求点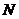 的坐标.
的坐标.
016]如图9,已知正比例函数和反比例函数的图象都经过点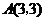 .
.
(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点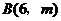 ,求
,求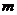 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与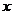 轴、
轴、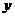 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
(4)在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积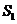 与四边形OABD的面积S满足:
与四边形OABD的面积S满足: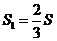 ?若存在,求点E的坐标;
?若存在,求点E的坐标;
若不存在,请说明理由.
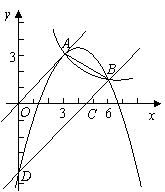
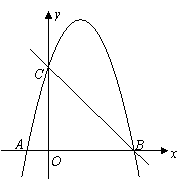
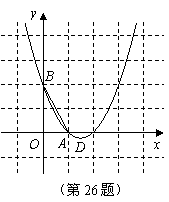
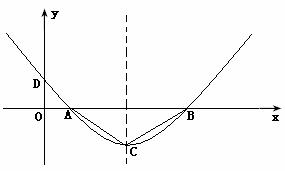
015]如图,二次函数的图象经过点D(0,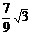 ),且顶点C的横坐标为4,该图象在x 轴上截得的线段AB的长为6.
),且顶点C的横坐标为4,该图象在x 轴上截得的线段AB的长为6.
⑴求二次函数的解析式;
⑵在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;
⑶在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com