
2、根据下面语境,为空格处选择合适的词语,将其序号填在横线上。(2分)
春夏秋冬,四季轮回,多少故事在雨中生动 ⑴ ,多少欢乐在嬉戏中尽情
⑵ ,多少温情在伞下默默 ⑶ ,多少憧憬在静寂中悄然 ⑷ 。
A.传递 B.绽放 C.孕育 D.演绎
21、(本小题满分14分)
在R上定义运算◎: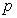 ◎
◎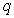 =
=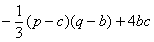 (
(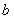 、
、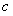 为实常数)。记
为实常数)。记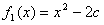 ,
,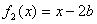 ,
, R,令
R,令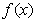 =
=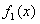 ◎
◎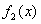 。
。
(1) 如果函数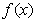 在
在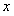 =1处有极值
=1处有极值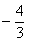 ,试确定
,试确定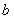 、
、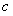 的值;
的值;
(2) 求曲线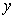 =
=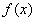 上斜率为
上斜率为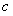 的切线与该曲线的公共点;
的切线与该曲线的公共点;
(3) 记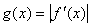 (-1≤
(-1≤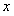 ≤1)的最大值为M,若M≥
≤1)的最大值为M,若M≥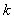 对任意的
对任意的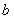 、
、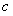 恒成立,试求
恒成立,试求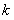 的最大值。
的最大值。
20、(本小题满分12分)
 A、B两城相距30km,现计划在两城外以 AB为直径的半圆弧AB上选择一点C建造垃圾处理厂,其对城A的影响度与厂址到城A的距离的平方成反比(比例系数
A、B两城相距30km,现计划在两城外以 AB为直径的半圆弧AB上选择一点C建造垃圾处理厂,其对城A的影响度与厂址到城A的距离的平方成反比(比例系数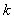 为正数),对城B的影响度也与厂址到城B的距离的平方成反比,且当厂址在弧AB的中点时,对城B的影响度是对城A的影响度的四倍,
为正数),对城B的影响度也与厂址到城B的距离的平方成反比,且当厂址在弧AB的中点时,对城B的影响度是对城A的影响度的四倍,
(1)试将总影响度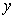 (对两城的影响度之和)表示成厂址到城A的距离
(对两城的影响度之和)表示成厂址到城A的距离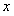 的函数;
的函数;
(2)是否存在一点,使建在此处的垃圾处理厂对两城的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
19、(本小题满分14分)
已知函数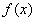 =
=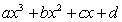 的单调递减区间是(-1,3),且在
的单调递减区间是(-1,3),且在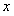 =1处的切线方程为:
=1处的切线方程为: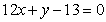
(1)、求函数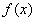 的解析式;
的解析式;
(2)、求函数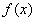 在区间[-4,4
]上的最值;
在区间[-4,4
]上的最值;
(3)、若过点(0,m)有且只有一条直线与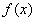 相切,求m的取值范围。
相切,求m的取值范围。
18、(本小题满分10分)
已知命题p:关于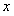 的方程
的方程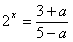 有负根 ; 命题q:不等式
有负根 ; 命题q:不等式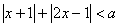 的解集为
的解集为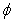 。且“p∨q”是真命题,“p∧q”是假命题,求实数
。且“p∨q”是真命题,“p∧q”是假命题,求实数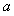 的取值范围。
的取值范围。
17、(本小题满分13分)
定义在(0,+∞)上的函数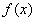 满足:对任意的
满足:对任意的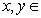 (0,+∞),都有
(0,+∞),都有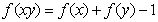 ,且当0<
,且当0<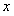 <1时, 都有
<1时, 都有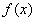 >1成立。
>1成立。
(1)、判断并证明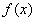 在定义域(0,+∞)上的单调性;
在定义域(0,+∞)上的单调性;
(2)、若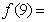 7,解不等式:
7,解不等式: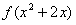 >4
>4
16、(本小题满分12分)
已知函数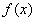 =
=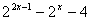 ,
,
(1)求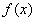 的零点;
的零点;
(2)求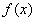 的值域。
的值域。







15、一辆汽车从静止状态开始启动前进,随即因故减速停车,其加速度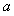 是时间
是时间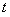 的函数:
的函数: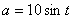 (单位:米/秒2),则该车从启动到停下来共前进了
米。
(单位:米/秒2),则该车从启动到停下来共前进了
米。

14、已知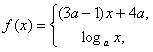
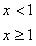 是R上的减函数,那么
是R上的减函数,那么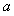 的取值范围是
。
的取值范围是
。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com