
4.The whole family were worried about Jane because no one was aware ___she had gone.
A.that where B.of the place which
C.of what D.of where
3.By the time he realizes he _____ into a trap, it'll be late for him to do anything about it.
A.walks B.walked C.has walked D.had walked
2.-Shall I keep an eye on your house when you are on holiday?
- .
A.It's up to you B.Of course you should
C.If you should like D.I would appreciate that.
第一节:多项选择(共l5小题;每小题l分,满分l5分)
从A、B、C、D四个选项中,选出可以填人空白处的最佳选项,并在答题卡上将该项涂黑。
1.An accident happened at______ crossroads a few metres away from ____bank.
A.a…a B./…a C./…the D.the…/
22.(本小题满分14分)
已知椭圆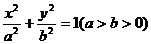 过点
过点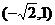 ,长轴长为
,长轴长为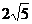 ,过点C(-1,0)且斜率为k的直线l与椭圆相交于不同的两点A、B.
,过点C(-1,0)且斜率为k的直线l与椭圆相交于不同的两点A、B.
(1)求椭圆的方程;
(2)若线段AB中点的横坐标是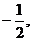 求直线l的斜率;
求直线l的斜率;
(3)在x轴上是否存在点M,使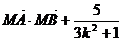 是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由.
是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由.
21.(本小题满分14分)
设函数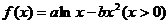
(1)若函数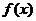 在x=1处与直线
在x=1处与直线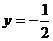 相切
相切
①求实数a,b的值;
②求函数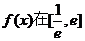 上的最大值.
上的最大值.
(2)当b=0时,若不等式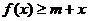 对所有的
对所有的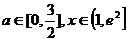 都成立,求实数m的取值范围.
都成立,求实数m的取值范围.
20.(本小题满分12分)
已知数列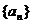 的前n项和为
的前n项和为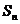 ,且满足
,且满足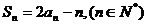
(1)求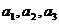 的值;
的值;
(2)求数列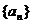 的通项公式;
的通项公式;
(3)若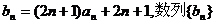 的前n项和为
的前n项和为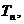 求满足不等式
求满足不等式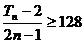 的最小n值.
的最小n值.
19.(本小题满分12分)
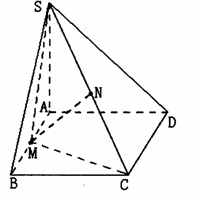
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥平面ABCD,二面角S-
CD-A的平面角为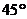 ,M为AB中点,N为SC中点.
,M为AB中点,N为SC中点.
(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SCD;
 (3)若
(3)若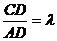 ,求实数
,求实数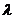 的值,使得直线SM与平面SCD所成角为
的值,使得直线SM与平面SCD所成角为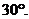
18.(本小题满分12分)
设O为坐标原点,点P的坐标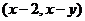
(I)在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最大值,并求事件“|OP|取到最大值”的概率;
(II)若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.
17.(本小题满分12分)
在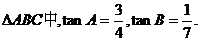
(1)求角C的大小;
(2)若AB边的长为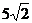 ,求BC边的长.
,求BC边的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com