
2.下列各组词语中,没有错别字的一组是 ( )
A.委曲 通讯社 寥若晨星 事实盛于雄辩
B.杀戳 综合症 娇揉造作 可望而不可即
C.装潢 飨读者 毁家纾难 化干戈为玉帛
D.和蔼 编者按 雪中送碳 水至清则无鱼
1.下列各项中,每对词语加点字读音完全不同的一组是 ( )
A.辟谣/精辟 犄角/掎角之势 丞待解决/岌岌可危
B.殉职/徇私 蹊跷/独辟蹊径 量入为出/质量并重
C.暗哑/谙熟 角色/崭露头角 载入史册/载人航天
D.剽悍/骠勇 混蛋/浑水摸鱼 重在参与/与人为善
010]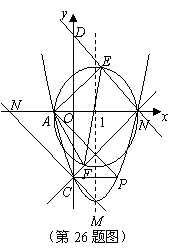 解:(1)根据题意,得
解:(1)根据题意,得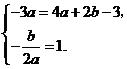 ···· 2分
···· 2分
解得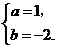
 抛物线对应的函数表达式为
抛物线对应的函数表达式为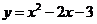 . 3分
. 3分
(2)存在.
在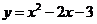 中,令
中,令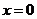 ,得
,得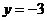 .
.
令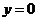 ,得
,得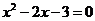 ,
,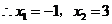 .
.
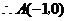 ,
,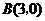 ,
,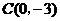 .
.
又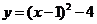 ,
, 顶点
顶点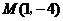 .········································································ 5分
.········································································ 5分
容易求得直线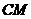 的表达式是
的表达式是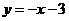 .
.
在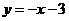 中,令
中,令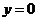 ,得
,得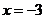 .
.
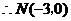 ,
,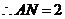 .···························································································· 6分
.···························································································· 6分
在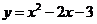 中,令
中,令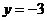 ,得
,得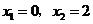 .
.
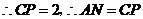 .
.
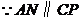 ,
, 四边形
四边形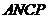 为平行四边形,此时
为平行四边形,此时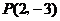 .································· 8分
.································· 8分
(3)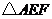 是等腰直角三角形.
是等腰直角三角形.
理由:在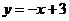 中,令
中,令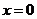 ,得
,得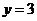 ,令
,令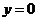 ,得
,得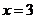 .
.
 直线
直线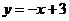 与坐标轴的交点是
与坐标轴的交点是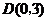 ,
,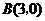 .
.
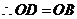 ,
,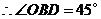 .·················································································· 9分
.·················································································· 9分
又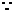 点
点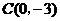 ,
,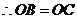 .
.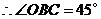 .··················································· 10分
.··················································· 10分
由图知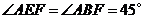 ,
,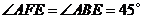 .·········································· 11分
.·········································· 11分
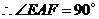 ,且
,且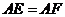 .
.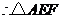 是等腰直角三角形.································· 12分
是等腰直角三角形.································· 12分
(4)当点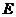 是直线
是直线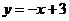 上任意一点时,(3)中的结论成立. 14分
上任意一点时,(3)中的结论成立. 14分
009]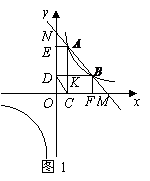 解:(1)①
解:(1)①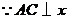 轴,
轴,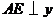 轴,
轴,
 四边形
四边形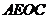 为矩形.
为矩形.
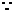
 轴,
轴,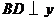 轴,
轴,
 四边形
四边形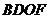 为矩形.
为矩形.
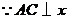 轴,
轴,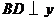 轴,
轴,
 四边形
四边形 均为矩形.············ 1分
均为矩形.············ 1分
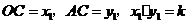 ,
,

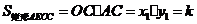
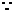
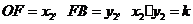 ,
,

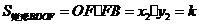 .
.

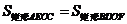 .
.
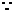
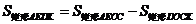 ,
,
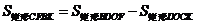 ,
,

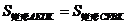 .······························································································ 2分
.······························································································ 2分
②由(1)知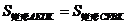 .
.

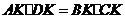 .
.

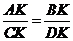 .············································································································ 4分
.············································································································ 4分
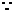
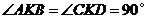 ,
,

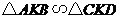 .································································································ 5分
.································································································ 5分

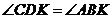 .
.

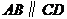 .············································································································· 6分
.············································································································· 6分
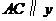 轴,
轴,
 四边形
四边形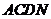 是平行四边形.
是平行四边形.

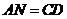 .············································································································· 7分
.············································································································· 7分
同理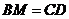 .
.
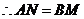 .············································································································· 8分
.············································································································· 8分
(2)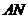 与
与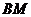 仍然相等.························································································· 9分
仍然相等.························································································· 9分
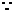
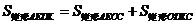 ,
,

 ,
,
又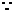
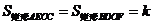 ,
,

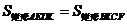 .································· 10分
.································· 10分

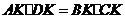 .
.

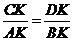 .
.
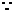
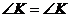 ,
,

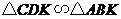 .
.

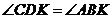 .
.

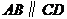 .············································································································ 11分
.············································································································ 11分
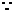
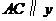 轴,
轴,
 四边形
四边形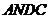 是平行四边形.
是平行四边形.

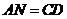 .
.
同理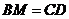 .
.

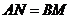 .·········································································································· 12分
.·········································································································· 12分
008]证明:(1)∵∠ABC=90°,BD⊥EC,
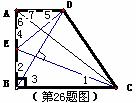 ∴∠1与∠3互余,∠2与∠3互余,
∴∠1与∠3互余,∠2与∠3互余,
∴∠1=∠2…………………………………………………1分
∵∠ABC=∠DAB=90°,AB=AC
∴△BAD≌△CBE…………………………………………2分
∴AD=BE……………………………………………………3分
(2)∵E是AB中点,
∴EB=EA由(1)AD=BE得:AE=AD……………………………5分
∵AD∥BC∴∠7=∠ACB=45°∵∠6=45°∴∠6=∠7
由等腰三角形的性质,得:EM=MD,AM⊥DE。
即,AC是线段ED的垂直平分线。……………………7分
(3)△DBC是等腰三角(CD=BD)……………………8分
理由如下:
由(2)得:CD=CE由(1)得:CE=BD∴CD=BD
∴△DBC是等腰三角形。……………………………10分
007]
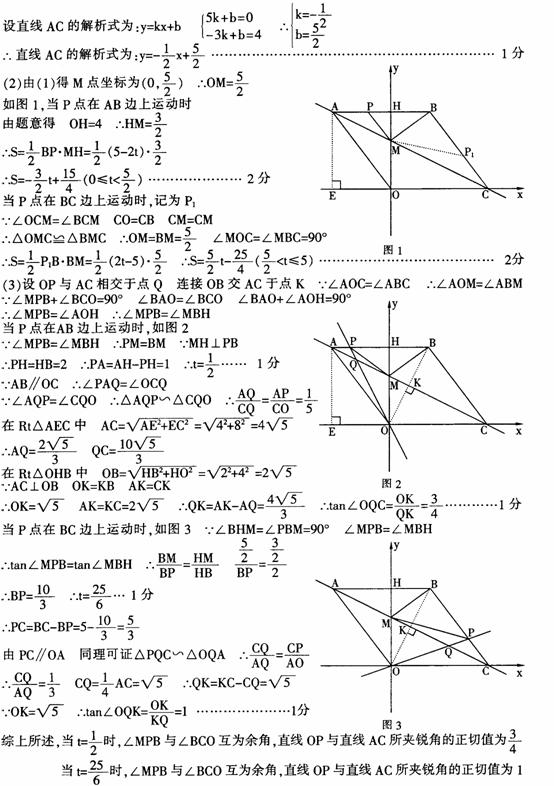
006]解:(1)OC=1,所以,q=-1,又由面积知0.5OC×AB=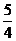 ,得AB=
,得AB=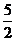 ,
,
设A(a,0),B(b,0)AB=b-a=
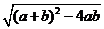 =
=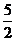 ,解得p=
,解得p=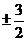 ,但p<0,所以p=
,但p<0,所以p=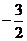 。
。
所以解析式为: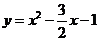
(2)令y=0,解方程得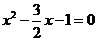 ,得
,得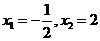 ,所以A(
,所以A(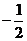 ,0),B(2,0),在直角三角形AOC中可求得AC=
,0),B(2,0),在直角三角形AOC中可求得AC=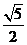 ,同样可求得BC=
,同样可求得BC=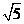 ,显然AC2+BC2=AB2,得△ABC是直角三角形。AB为斜边,所以外接圆的直径为AB=
,显然AC2+BC2=AB2,得△ABC是直角三角形。AB为斜边,所以外接圆的直径为AB=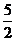 ,所以
,所以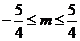 。
。
(3)存在,AC⊥BC,①若以AC为底边,则BD//AC,易求AC的解析式为y=-2x-1,可设BD的解析式为y=-2x+b,把B(2,0)代入得BD解析式为y=-2x+4,解方程组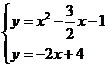 得D(
得D(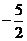 ,9)
,9)
②若以BC为底边,则BC//AD,易求BC的解析式为y=0.5x-1,可设AD的解析式为y=0.5x+b,把 A(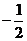 ,0)代入得AD解析式为y=0.5x+0.25,解方程组
,0)代入得AD解析式为y=0.5x+0.25,解方程组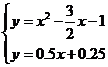 得D(
得D(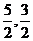 ) 综上,所以存在两点:(
) 综上,所以存在两点:(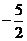 ,9)或(
,9)或(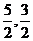 )。
)。
004](1)解:由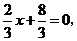 得
得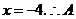 点坐标为
点坐标为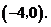
由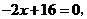 得
得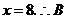 点坐标为
点坐标为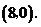 ∴
∴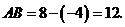 (2分)
(2分)
由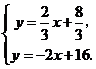 解得
解得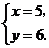 ∴
∴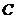 点的坐标为
点的坐标为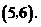 (3分)
(3分)
∴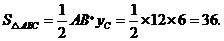 (4分)
(4分)
(2)解:∵点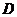 在
在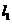 上且
上且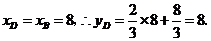 ∴
∴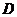 点坐标为
点坐标为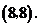 (5分)又∵点
(5分)又∵点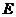 在
在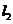 上且
上且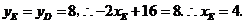 ∴
∴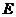 点坐标为
点坐标为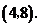 (6分)
(6分)
∴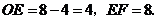 (7分)
(7分)
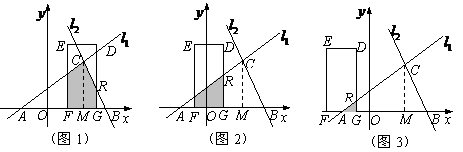
(3)解法一: 当
当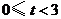 时,如图1,矩形
时,如图1,矩形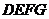 与
与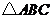 重叠部分为五边形
重叠部分为五边形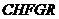 (
(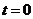 时,为四边形
时,为四边形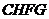 ).过
).过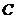 作
作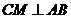 于
于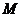 ,则
,则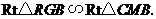
∴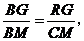 即
即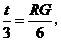 ∴
∴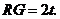
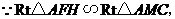
∴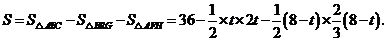
即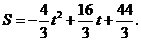 (10分)
(10分)
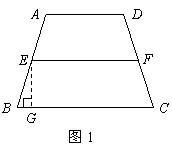 [005](1)如图1,过点
[005](1)如图1,过点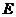 作
作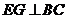 于点
于点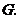 ·················· 1分
·················· 1分
∵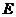 为
为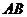 的中点,
的中点,
∴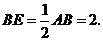
在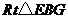 中,
中,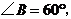 ∴
∴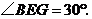 ············· 2分
············· 2分
∴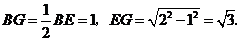
即点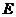 到
到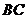 的距离为
的距离为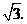 ··········································· 3分
··········································· 3分
(2)①当点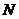 在线段
在线段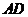 上运动时,
上运动时,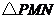 的形状不发生改变.
的形状不发生改变.
∵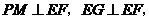 ∴
∴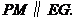
∵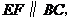 ∴
∴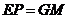 ,
,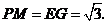
同理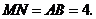 ······························································································· 4分
······························································································· 4分
如图2,过点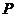 作
作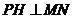 于
于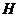 ,∵
,∵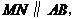
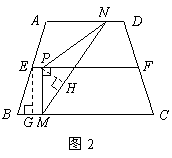 ∴
∴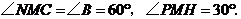
∴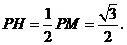
∴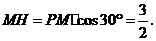
则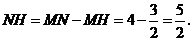
在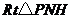 中,
中,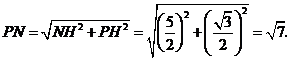
∴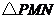 的周长=
的周长=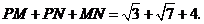 ············································· 6分
············································· 6分
②当点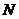 在线段
在线段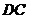 上运动时,
上运动时,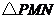 的形状发生改变,但
的形状发生改变,但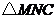 恒为等边三角形.
恒为等边三角形.
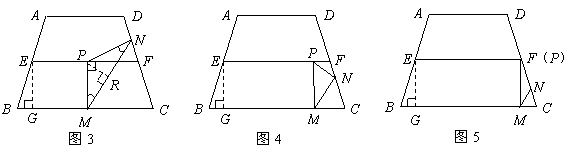
当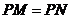 时,如图3,作
时,如图3,作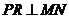 于
于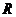 ,则
,则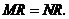
类似①,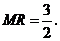
∴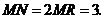 ································································································ 7分
································································································ 7分
∵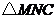 是等边三角形,∴
是等边三角形,∴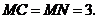
此时,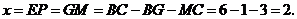 ········································· 8分
········································· 8分
 当
当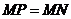 时,如图4,这时
时,如图4,这时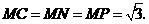
此时,
当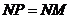 时,如图5,
时,如图5,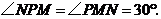
则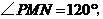 又
又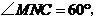
∴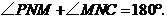
因此点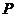 与
与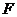 重合,
重合,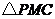 为直角三角形.
为直角三角形.
∴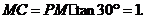
此时,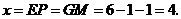
综上所述,当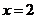 或4或
或4或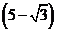 时,
时, 为等腰三角形.
为等腰三角形.
003]解.(1)点A的坐标为(4,8) …………………1分
将A (4,8)、C(8,0)两点坐标分别代入y=ax2+bx
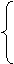 8=16a+4b
8=16a+4b
得
0=64a+8b
解 得a=-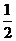 ,b=4
,b=4
∴抛物线的解析式为:y=-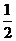 x2+4x …………………3分
x2+4x …………………3分
(2)①在Rt△APE和Rt△ABC中,tan∠PAE=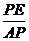 =
=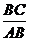 ,即
,即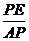 =
=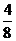
∴PE=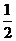 AP=
AP=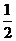 t.PB=8-t.
t.PB=8-t.
∴点E的坐标为(4+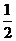 t,8-t).
t,8-t).
∴点G的纵坐标为:-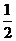 (4+
(4+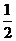 t)2+4(4+
t)2+4(4+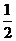 t)=-
t)=-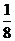 t2+8. …………………5分
t2+8. …………………5分
∴EG=-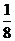 t2+8-(8-t) =-
t2+8-(8-t) =-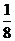 t2+t.
t2+t.
∵-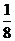 <0,∴当t=4时,线段EG最长为2.
…………………7分
<0,∴当t=4时,线段EG最长为2.
…………………7分
②共有三个时刻. …………………8分
t1=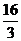 , t2=
, t2=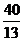 ,t3=
,t3= 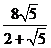 .
…………………11分
.
…………………11分
002]解:(1)1,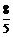 ;
;
(2)作QF⊥AC于点F,如图3, AQ = CP= t,∴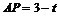 .
.
 由△AQF∽△ABC,
由△AQF∽△ABC,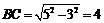 ,
,
得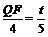 .∴
.∴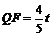 . ∴
. ∴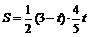 ,
,
即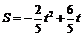 .
.
(3)能.
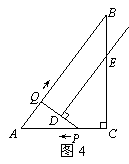
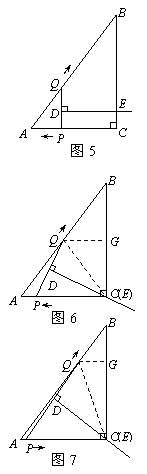 ①当DE∥QB时,如图4.
①当DE∥QB时,如图4.
∵DE⊥PQ,∴PQ⊥QB,四边形QBED是直角梯形.
此时∠AQP=90°.
由△APQ ∽△ABC,得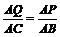 ,
,
即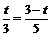 . 解得
. 解得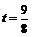 .
.
②如图5,当PQ∥BC时,DE⊥BC,四边形QBED是直角梯形.
此时∠APQ =90°.
由△AQP ∽△ABC,得 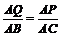 ,
,
即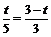 . 解得
. 解得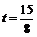 .
.
(4)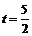 或
或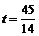 .
.
[注:①点P由C向A运动,DE经过点C.
方法一、连接QC,作QG⊥BC于点G,如图6.
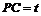 ,
,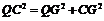
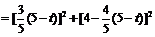 .
.
由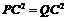 ,得
,得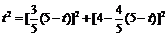 ,解得
,解得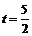 .
.
方法二、由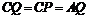 ,得
,得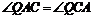 ,进而可得
,进而可得
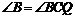 ,得
,得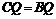 ,∴
,∴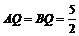 .∴
.∴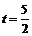 .
.
②点P由A向C运动,DE经过点C,如图7.
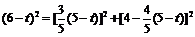 ,
,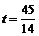 ]
]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com