
5.函数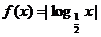 的单调递增区间是( )
的单调递增区间是( )
A 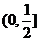 B
B 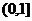 C (0,+∞) D
C (0,+∞) D 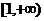
4. 若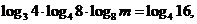 则
则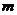 =( )
=( )
A 8 B 9 C 81 D 16
3.下列函数中哪个是幂函数( )
A.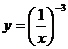 B.
B.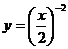 C.
C.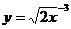 D.
D.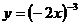
2.已知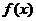 的定义域为
的定义域为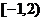 ,则
,则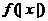 的定义域为( )
的定义域为( )
A.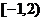 B.
B.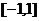 C.
C.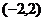 D.
D.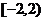
1.已知集合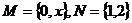 ,若
,若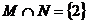 ,则
,则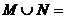 (
)
(
)
A.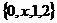 B.
B.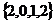 C.
C.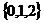 D.不能确定
D.不能确定
2.在研究增长问题、复利问题、质量浓度问题中常见这类函数.
例题:某地现有森林面积为1000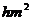 ,每年增长5%,经过
,每年增长5%,经过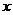
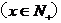 年,森林面积为
年,森林面积为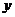
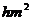 .写出
.写出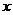 ,
,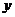 间的函数关系式,并求出经过5年,森林的面积.
间的函数关系式,并求出经过5年,森林的面积.
分析:要得到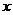 ,
,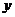 间的函数关系式,可以先一年一年的增长变化,找出规律,再写出
间的函数关系式,可以先一年一年的增长变化,找出规律,再写出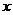 ,
,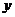 间的函数关系式.
间的函数关系式.
解: 根据题意,经过一年, 森林面积为1000(1+5%)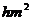 ;经过两年,
森林面积为1000(1+5%)2
;经过两年,
森林面积为1000(1+5%)2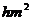 ;经过三年,
森林面积为1000(1+5%)3
;经过三年,
森林面积为1000(1+5%)3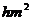 ;所以
;所以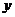 与
与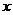 之间的函数关系式为
之间的函数关系式为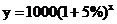
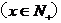 ,经过5年,森林的面积为1000(1+5%)5=1276.28(hm2).
,经过5年,森林的面积为1000(1+5%)5=1276.28(hm2).
练习:课本练习1,2
补充例题:高一某学生家长去年年底到银行存入2000元,银行月利率为2.38%,那么如果他第n个月后从银行全部取回,他应取回钱数为y,请写出n与y之间的关系,一年后他全部取回,他能取回多少?
解:一个月后他应取回的钱数为y=2000(1+2.38%),二个月后他应取回的钱数为y=2000(1+2.38%)2;,三个月后他应取回的钱数为y=2000(1+2.38%)3,…, n个月后他应取回的钱数为y=2000(1+2.38%)n; 所以n与y之间的关系为y=2000(1+2.38%)n (n∈N+),一年后他全部取回,他能取回的钱数为y=2000(1+2.38%)12.
补充练习:某工厂年产值逐年按8%的速度递增,今年的年产值为200万元,那么第n年后该厂的年产值为多少?
课后作业:课本习题3-1 1,2,3
1.正整数指数函数的图像是一些孤立的点,这是因为函数的定义域是正整数集.
3、情感.态度与价值观
使学生通过学习正整数指数函数体会学习指数函数的重要意义,增强学习研究函数的积极性和自信心.
[教学重点]: 正整数指数函数的定义.
[教学难点]:正整数指数函数的解析式的确定.
[教学教具]:直尺、多媒体
[课时安排]: 1课时
[学法指导]:学生观察、思考、探究.
[讲授过程]
 [新课导入]
[新课导入]
[互动过程1]
(1)请你用列表表示1个细胞分裂次数分别为1,2,3,4,5,6,7,8时,
得到的细胞个数;
(2)请你用图像表示1个细胞分裂的次数n(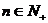 )与得到的细
)与得到的细
胞个数y之间的关系;
(3)请你写出得到的细胞个数y与分裂次数n之间的关系式,试用
科学计算器计算细胞分裂15次、20次得到的细胞个数.
解:(1)利用正整数指数幂的运算法则,可以算出1个细胞分裂1,2,3,
4,5,6,7,8次后,得到的细胞个数
|
分裂次数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
细胞个数 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
(2)1个细胞分裂的次数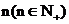 与得到的细胞个数
与得到的细胞个数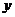 之间的关系可以用图像表示,它的图像是由一些孤立的点组成
之间的关系可以用图像表示,它的图像是由一些孤立的点组成
(3)细胞个数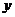 与分裂次数
与分裂次数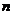 之间的关系式为
之间的关系式为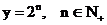 ,用科学计算器算得
,用科学计算器算得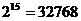 ,
,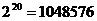

所以细胞分裂15次、20次得到的细胞个数分别为32768和1048576.
探究:从本题中得到的函数来看,自变量和函数值分别是什么?此函数是什么类型的函数? 细胞个数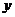 随着分裂次数
随着分裂次数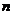 发生怎样变化?你从哪里看出?
发生怎样变化?你从哪里看出?
小结:从本题中可以看出我们得到的细胞分裂个数都是底数为2的指数,而且指数是变量,取值为正整数. 细胞个数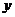 与分裂次数
与分裂次数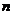 之间的关系式为
之间的关系式为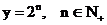 .细胞个数
.细胞个数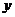 随着分裂次数
随着分裂次数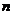 的增多而逐渐增多.
的增多而逐渐增多.
[互动过程2]
问题2.电冰箱使用的氟化物的释放破坏了大气上层的臭氧层,臭氧含量Q近似满足关系式Q=Q00.9975 t,其中Q0是臭氧的初始量,t是时间(年),这里设Q0=1.
(1)计算经过20,40,60,80,100年,臭氧含量Q;
(2)用图像表示每隔20年臭氧含量Q的变化;
(3)试分析随着时间的增加,臭氧含量Q是增加还是减少.
解:(1)使用科学计算器可算得,经过20,40,60,80,100年,臭氧含量Q的值分别为0.997520=0.9512, 0.997540=0.9047, 0.997560=0.8605, 0.997580=0.8185, 0.9975100=0.7786;
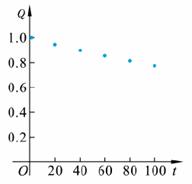 (2)用图像表示每隔20年臭氧含量Q的变化如图所
(2)用图像表示每隔20年臭氧含量Q的变化如图所
示,它的图像是由一些孤立的点组成.
(3)通过计算和观察图形可以知道, 随着时间的增加,
臭氧含量Q在逐渐减少.
探究:从本题中得到的函数来看,自变量和函数值分别
又是什么?此函数是什么类型的函数?,臭氧含量Q随着
时间的增加发生怎样变化?你从哪里看出?
小结:从本题中可以看出我们得到的臭氧含量Q都是
底数为0.9975的指数,而且指数是变量,取值为正整数.
臭氧含量Q近似满足关系式Q=0.9975 t,
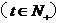 随着时间的增加,臭氧含量Q在逐渐减少.
随着时间的增加,臭氧含量Q在逐渐减少.
[互动过程3]
上面两个问题所得的函数有没有共同点?你能统一吗?自变量的取值范围又是什么?这样的函数图像又是什么样的?为什么?
正整数指数函数的定义:
一般地,函数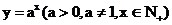 叫作正整数指数函数,其中
叫作正整数指数函数,其中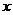 是自变量,定义域是正整数集
是自变量,定义域是正整数集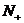 .
.
说明:
2、 过程与方法
(1)让学生借助实例,了解正整数指数函数,体会从具体到一般,从个别到整体的研究过程和研究方法.
(2)从图像上观察体会正整数指数函数的性质,为这一章的学习作好铺垫.
1、知识与技能
(1) 结合实例,了解正整数指数函数的概念.
(2)能够求出正整数指数函数的解析式,进一步研究其性质.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com