
5.如果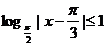 ,那么
,那么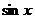 的取值范围是( )
的取值范围是( )
A.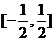 B.
B.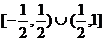 C.
C. 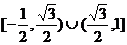 D.
D.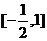
4.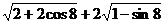 的简化结果为( )
的简化结果为( )
A.4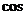 4-2sin4
B.2sin4 C.2sin4-4
4-2sin4
B.2sin4 C.2sin4-4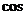 4
D.-2sin4
4
D.-2sin4
3.函数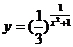 的值域为( )
的值域为( )
A.(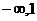 ) B.(
) B.(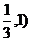 C.
C.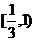 D.
D.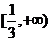
2.为了得到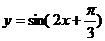 的图象,只需将
的图象,只需将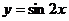 的图象( )
的图象( )
A.向左平移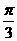 个单位 B.向右平移
个单位 B.向右平移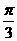 个单位
个单位
C.向左平移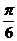 个单位 D.向右平移
个单位 D.向右平移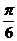 个单位
个单位
1.满足集合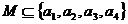 ,且
,且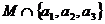 =
=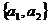 的集合
的集合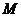 的个数是( )
的个数是( )
A.1 B.2 C.3 D.4
例5.求中心在原点,一个焦点为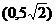 且被直线
且被直线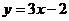 截得的弦中点横坐标为
截得的弦中点横坐标为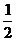 的椭圆方程.
的椭圆方程.
解: 设椭圆方程 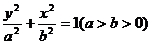 ,
,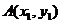 ,
,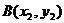 ,
,
因为弦AB中点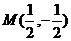 ,所以
,所以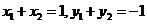

由 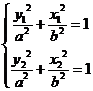 得
得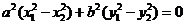 ,(点差法)
,(点差法)
所以 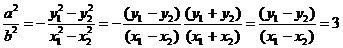
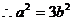 又
又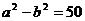
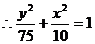

例6椭圆Q: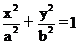 (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点。求点P的轨迹H的方程
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点。求点P的轨迹H的方程
解:设椭圆Q: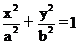 (a>b>0)
(a>b>0)
上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则
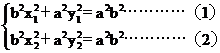
1°当AB不垂直x轴时,x1¹x2,由(1)-(2)得b2(x1-x2)2x+a2(y1-y2)2y=0
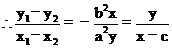 \b2x2+a2y2-b2cx=0…………(3)
\b2x2+a2y2-b2cx=0…………(3)
2°当AB垂直于x轴时,点P即为点F,满足方程(3)
故所求点P的轨迹方程为:b2x2+a2y2-b2cx=0
例7如图,椭圆 上的点M与椭圆右焦点F1的连线MF1与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.(1)求椭圆的离心率;(2)F2是椭圆的左焦点,C是椭圆上的任一点,证明:∠F1CF2≤ ;
上的点M与椭圆右焦点F1的连线MF1与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.(1)求椭圆的离心率;(2)F2是椭圆的左焦点,C是椭圆上的任一点,证明:∠F1CF2≤ ; 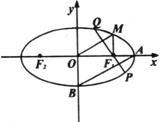 (3)过F1且与AB垂直的直线交椭圆于P、Q,若△PF2Q的面积是20 ,求此时椭圆的方程.
(3)过F1且与AB垂直的直线交椭圆于P、Q,若△PF2Q的面积是20 ,求此时椭圆的方程.
(1)易得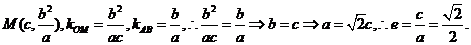
(2)证:由椭圆定义得: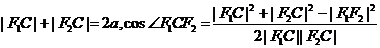
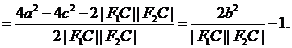
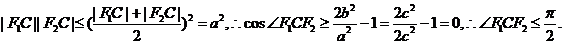 (3)解:设直线PQ的方程为
(3)解:设直线PQ的方程为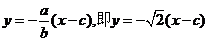 .代入椭圆方程消去x得:
.代入椭圆方程消去x得: 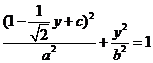 ,整理得:
,整理得: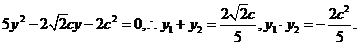
∴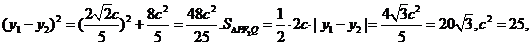
因此a2=50,b2=25,所以椭圆方程为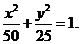
例2.如图,直线y=kx+b与椭圆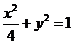 交于A、B两点,记△AOB的面积为S. (I)求在k=0,0<b<1的条件下,S的最大值;
(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.
交于A、B两点,记△AOB的面积为S. (I)求在k=0,0<b<1的条件下,S的最大值;
(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.
本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.满分15分.
(I)解:设点A的坐标为(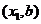 ,点B的坐标为
,点B的坐标为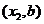 ,
,
由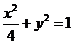 ,解得
,解得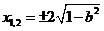
所以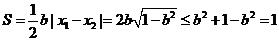
当且仅当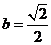 时,.S取到最大值1.
时,.S取到最大值1.
(Ⅱ)解:由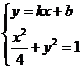 得
得
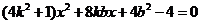
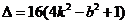 ①
①
|AB|=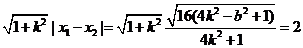 ②
②
又因为O到AB的距离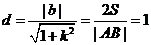 所以
所以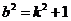 ③
③
③代入②并整理,得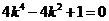
解得,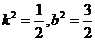 ,代入①式检验,△>0
,代入①式检验,△>0
故直线AB的方程是
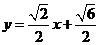 或
或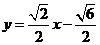 或
或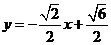 或
或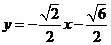 .例例例3.已知椭圆C:
.例例例3.已知椭圆C: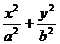 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为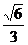 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为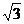 . (Ⅰ)求椭圆C的方程; (Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为
. (Ⅰ)求椭圆C的方程; (Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为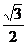 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
解:(Ⅰ)设椭圆的半焦距为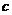 ,依题意
,依题意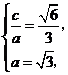
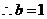 ,
,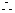 所求椭圆方程为
所求椭圆方程为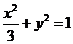 .
.
(Ⅱ)设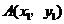 ,
,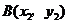 .(1)当
.(1)当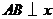 轴时,
轴时,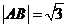 .
.
(2)当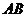 与
与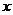 轴不垂直时,设直线
轴不垂直时,设直线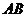 的方程为
的方程为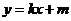 .
.
由已知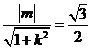 ,得
,得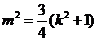 .
.
把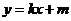 代入椭圆方程,整理得
代入椭圆方程,整理得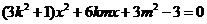 ,
,
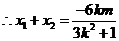 ,
,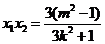 .
.
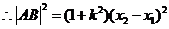
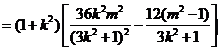
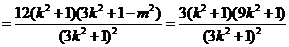
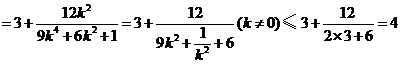 .
.
当且仅当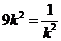 ,即
,即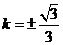 时等号成立.当
时等号成立.当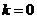 时,
时,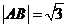 ,
,
综上所述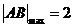 .
. 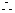 当
当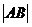 最大时,
最大时,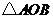 面积取最大值
面积取最大值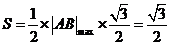 .
.
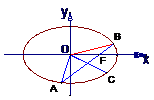 例 4 如图 ,椭圆的中心在原点, 焦点在x轴上, 过其右焦点F作斜率为1的直线, 交椭圆于A、B两点, 若椭圆上存在一点C, 使
例 4 如图 ,椭圆的中心在原点, 焦点在x轴上, 过其右焦点F作斜率为1的直线, 交椭圆于A、B两点, 若椭圆上存在一点C, 使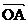 +
+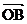 =
=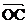 . (1) 求椭圆的离心率;(2) 若
. (1) 求椭圆的离心率;(2) 若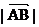 =15, 求着个椭圆的方程.
=15, 求着个椭圆的方程.
解: (1)设椭圆的方程为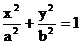 , 焦距为
, 焦距为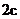 , 则直线l的方程为:
, 则直线l的方程为: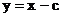 ,
,
代入椭圆方程,
得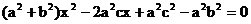 ,
,
设点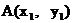 、
、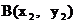 ,
,
则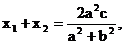
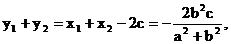 ∵
∵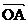 +
+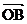
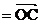 , ∴C点坐标为
, ∴C点坐标为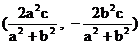 .∵C点在椭圆上, ∴
.∵C点在椭圆上, ∴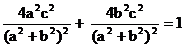 .
.
∴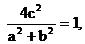 ∴
∴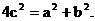 又
又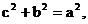 ∴
∴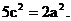 ∴
∴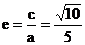
(2) ∵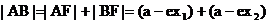
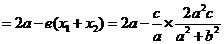
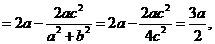
由已知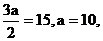 从而
从而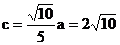 . ∴
. ∴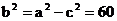 .
.
故椭圆的方程为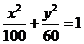
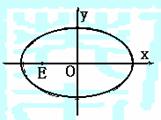
例1 已知方向向量为v=(1,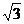 )的直线l过点(0,-2
)的直线l过点(0,-2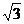 )和椭圆C:
)和椭圆C: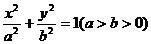 的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
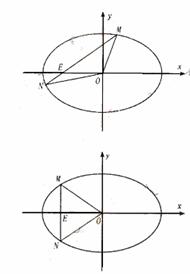
(Ⅰ)求椭圆C的方程;(Ⅱ)是否存在过点E(-2,0)的直线m交椭圆C于点M、N,满足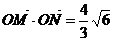 cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
(I)解法一:直线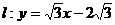 , ①
, ①
过原点垂直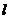 的直线方程为
的直线方程为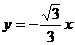 , ②
, ②
解①②得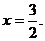
∵椭圆中心O(0,0)关于直线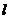 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
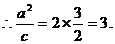
∵直线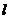 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).
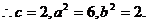 故椭圆C的方程为
故椭圆C的方程为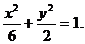 ③
③
解法二:直线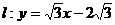 .
.
设原点关于直线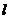 对称点为(p,q),则
对称点为(p,q),则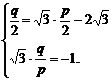 解得p=3.
解得p=3.
∵椭圆中心O(0,0)关于直线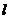 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
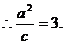 ∵直线
∵直线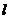 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).
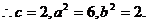 故椭圆C的方程为
故椭圆C的方程为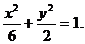 ③
③
(II)解法一:设M(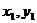 ),N(
),N(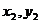 ).
).
当直线m不垂直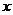 轴时,直线
轴时,直线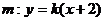 代入③,整理得
代入③,整理得
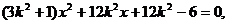
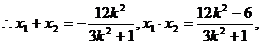
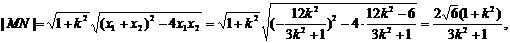
点O到直线MN的距离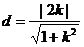
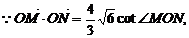 即
即 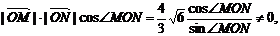
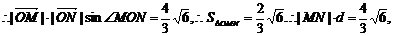
即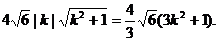
整理得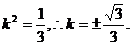
当直线m垂直x轴时,也满足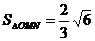 .
.
故直线m的方程为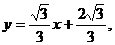
或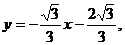 或
或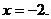
经检验上述直线均满足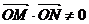 .
.
所以所求直线方程为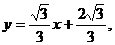 或
或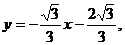 或
或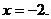
解法二:设M(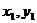 ),N(
),N(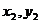 ).
).
当直线m不垂直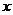 轴时,直线
轴时,直线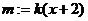 代入③,整理得
代入③,整理得
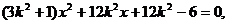
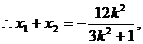
∵E(-2,0)是椭圆C的左焦点,
∴|MN|=|ME|+|NE|
=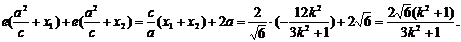
以下与解法一相同.
解法三:设M(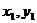 ),N(
),N(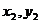 ).
).
设直线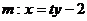 ,代入③,整理得
,代入③,整理得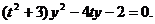
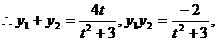
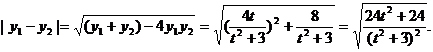
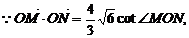 即
即 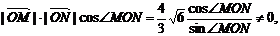
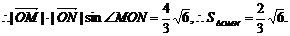
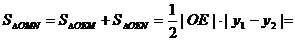
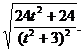
∴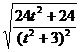 =
=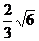 ,整理得
,整理得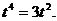
解得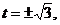 或
或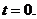
故直线m的方程为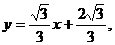 或
或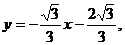 或
或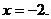
经检验上述直线方程为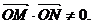
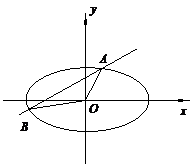 所以所求直线方程为
所以所求直线方程为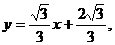 或
或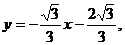 或
或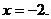
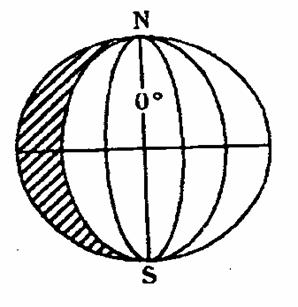
32.读图(阴影部分为黑夜),回答下列各问题(12分):
(1)此时太阳直射点的地理坐标 。
(2)此时地球上除日界线(180°经线)两侧日期不同外,还有一条经线的东西两侧日期也不相同,这条经线是 。
(3)此时所示的白天与黑夜的交界线是 (晨线、昏线);
若自南极沿20°W经线作水平运动物体,落于赤道处时,它位于 半球。

31.读图8“地球公转示意图”和“极地投影图”,回答下列问题:(18分)
(1)图甲中的A、B、C、D四点中最接近公转轨道上近日点的是 ,此时,地球公转速度较 ,我国正值一年中的 季。
(2)当地球由A向B公转的过程中,北半球各地 (选择填空)。
A.白昼渐长,黑夜渐短 B.极夜范围逐渐扩大
C.正午太阳高度逐渐变大 D.白昼渐短,黑夜渐长
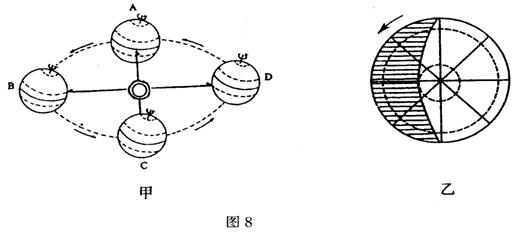
(3)观察图乙。有关此日某些地理现象的叙述,正确的是 (选择填空)。
A.太阳入射光线与地轴垂直
B.晨昏线与极圈相切
C. 晨昏线与地轴重合
D.太阳直射点上的入射光线的延长线过地心且与赤道平面有23.5°的夹角
(4)当地球公转到D点时, (选择填空)。
A.北半球正午太阳高度达到最小值 B.全球各地昼夜等长
 C.北半球昼长夜短 D.此时不适合去南极考察
C.北半球昼长夜短 D.此时不适合去南极考察
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com