
2. 若全集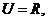 且
且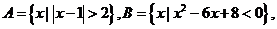 则
则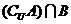 等于( )
等于( )
A. 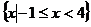 B.
B. 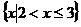 C.
C. 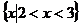 D.
D. 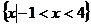
1. 下列说法正确的是( )
A. 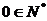 B.
B.
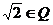 C.
C.
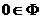 D.
D.
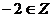
(二)认识自我的途径(板书)
学生活动:先分组活动,各组由一名同学负责,每位同学先将前面填过的优点缺点表格展示给大家,其他同学在此基础上提出自己的意见。每位同学对比自己眼中的“我”和别人眼中的“我”有何不同。然后各组将结果在全班内交流,再由其他同学进行评价。通过此活动,让学生了解正确认识自己的途径。
1、通过自我观察认识自己。
2、通过他人了解自己。
3、通过集体了解自己。
每位同学记录活动结果,全面认识自己。并以此为参考,经常自我检查,努力保持和发挥优势,改进不足,不断更新和完善自我。请记住,认识自我,你就是一座金矿,拥有自信、自主、自爱,你就一定能够在自己的人生中展出现应有的风采。
小结:
诗朗诵《我就是我》
一
我就是我
女孩的体魄
男孩的性格
十四岁肆意挥霍
喜怒哀乐
二
脚下的路
无论多么坎坷
摔倒爬起
依然是
洒脱的我
即使置身于痛苦的世界
也不乞求怜悯与施舍
宁愿用稚嫩的手
把未来的道路开拓
三
失败与成功
--黎明与黑暗的拼搏
每天的太阳
都在我手中捧出
微笑与欢乐
不会无偿地给予
阳光和草地
可供我小憩
岁月和年华
在急剧流失
不去贪恋逗留
也不曾沉没
因为明天
还有片片荒漠
让我去播种绿色
教案点评:
本节课的设计以学生活动为主,再辅以讲故事、电影片段欣赏等多种形式,教学内容比较丰富,让学生在活跃的课堂气氛中真切认识自己。

















(一)自我新认识(板书)
也许很多同学会说,世上最了解自己的莫过于自己,我当然认识自己了。但事实是否如此呢?文学家苏轼写到“不识庐山真面目,只缘身在此山中。”认识自己有时比认识别人可能更要困难。
那么,怎样才能正确认识自己呢?
1、要全面认识自己。(板书)
学生活动:联系教材上的事例及电影《巴黎圣母院》片段,进行如下讨论:
你判断一个人“美”的标准是什么?
人的内在美与外在美有什么联系吗?
通过讨论,总结出一个人的美应是外在美与内在美的和谐统一,内在美对外在美起促进作用。
每个人的外在形象与内在素质都存在着自己的优势与不足,全面认识自己,既要看到自己的优点,也要看到自己的缺点。
学生活动:填表
我的优点
我的不足
1、
1、
2、
2、
……
……
正所谓“金无足赤,人无完人”,我们每个人都有自己的缺点,但同时,每个人也都有自己的闪光点。当然,我们不必为此沮丧,也不必为此沾沾自喜。同学们可以看看下面两个故事,体会一下应该如何对待自己的优缺点。
《孔雀和朱娜》:孔雀向天后诉苦,说夜莺以她的歌取悦每个人的耳朵,而她的声音非常难听,别人都笑话她。朱娜安慰她,说她有美丽的羽毛是别的鸟儿所不能比的,但孔雀还是很伤心,最后在悲观绝望中死去。
《橄榄树和无花果》:橄榄树笑无花果随着季节的变化而换叶,一阵大雪下下来,无花果因为落尽了叶子,雪就无法落在它身上。而橄榄树满树都是叶,雪就落到它的枝桠上,压断了它的枝桠,夺去了它的美丽和生命。
事物总是发展变化的,没有一成不变的事物。因此,我们在全面认识自己的同时,还要用发展的眼光看自己。
2、用发展的眼光看待自己。(板书)
故事:《白纸黑点与黑纸白点》
在非洲加纳的一所寄宿制中学里,一位老师走进了教室。他先拿出了一张画有一个黑点的白纸,问他的学生:“孩子们,你们看到了什么?”学生们盯住黑点,齐声喊到:“一个黑点”。老师非常沮丧。“难道你们谁也没有看到这张白纸吗?眼光集中在黑点上,黑点会越来越大。生活中你们可不要这样啊!”教室里鸦雀无声。老师又拿出一张黑纸,中间有一个白点。他问他的学生“孩子们,你们又看到了什么?”学生齐声回答:“一个白点”。老师高兴地笑了:“孩子们太好了,无限美好的未来在等着你们。”
学生讨论:(如下观点可供参考)
第一次孩子们只看到了白纸上的黑点,老师很沮丧,因为这表明孩子们对自身认识不够,遇到挫折时容易自卑。第二次孩子们看到了黑纸中的白点,说明学生遇到挫折时还能看到自己好的一面,是乐观的、不畏挫折的,因此老师高兴地笑了。
这个故事给我的启发是,我们应多关注自己的优点和长处,要用欣赏的目光来看自己,即使你可能有很多不足,因为只有先看得起自己,才能正确认识自己。
面对纷繁复杂的人生世界,如果你把目光都集中在痛苦、烦恼上,生命就会黯然失色;如果你把目光都转移到快乐之中,你将会得到幸福。同样的道理,面对自己,如果你只看到自己的缺点、不足,你将会悲观绝望,停步不前;如果你能看到自己的优点、长处,你将会充满信心,迎接生活的挑战。
学生活动:分组活动,介绍自己近一两年来在习惯、性格、学识、能力等方面的变化。
习惯方面的变化:_______________________
学识方面的增长:_______________________
性格方面的变化:_______________________
能力方面的提高:_______________________
总结出:每个人都是不断变化发展的,自身的优点、缺点也不是一成不变的。我们要用发展的眼光看待自己,通过不断改正缺点来完善自己。
21.(本小题14分)
已知函数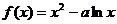 在(1,2]上是增函数。
在(1,2]上是增函数。
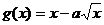 在(0,1)上减函数。
在(0,1)上减函数。
(1)求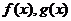 的表达式。
的表达式。
(2)当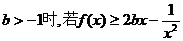 在
在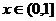 内恒成立,求实数
内恒成立,求实数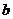 的取值范围。
的取值范围。
(3)求证:当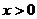 时,方程
时,方程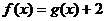 有唯一解。
有唯一解。

 安徽省无为中学(2009-2010-1)第二次检测试卷
安徽省无为中学(2009-2010-1)第二次检测试卷
20.(本小题13分)
对于三次函数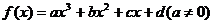

 定义:
定义:
(1)设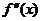 是函数
是函数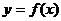 的导函数
的导函数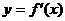 的导数。若方程
的导数。若方程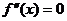 有实数解
有实数解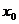 ,则称点
,则称点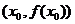 为函数
为函数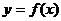 的“拐点”。
的“拐点”。
(2)设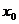 为常数,若定义在R上的函数
为常数,若定义在R上的函数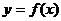 对于定义域内的一切实数
对于定义域内的一切实数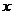 ,都有
,都有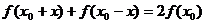 成立。则函数
成立。则函数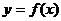 的图象关于点
的图象关于点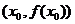 对称
对称
已知:
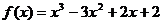
(1)求函数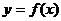 的“拐点”A的坐标。
的“拐点”A的坐标。
(2)检验函数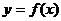 的图象是否关于“拐点”A对称。并对任意一个三次函数,写出一个有关“拐点”的结论(不必证明)
的图象是否关于“拐点”A对称。并对任意一个三次函数,写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数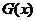 ,使它的“拐点”为(-1,3),(不写过程)
,使它的“拐点”为(-1,3),(不写过程)
19.(本小题12分)已知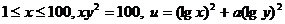
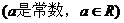 ①写出
①写出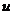 关于
关于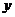 的函数解析式。
的函数解析式。
② 求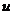 的最大值与最小值。
的最大值与最小值。
18.(本小题12分),在△ABC中,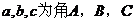 的对边,已知
的对边,已知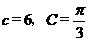
①△ABC的面积为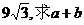
②若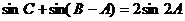 ,求△ABC的面积
,求△ABC的面积
17.(本小题12分)设二次函数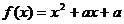 方程
方程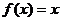 的两根为
的两根为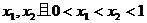
(1)求实数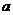 的范围
的范围
(2)试比较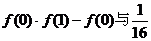 的大小,并说明理由。
的大小,并说明理由。
16.(本小题12分),已知函数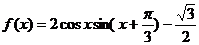
(1)求函数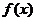 的最小正周期
的最小正周期
(2)在给定的坐标系中,作出函数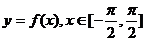 的图象。
的图象。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com