
13.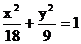
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
理 |
文 |
理 |
文 |
||||||||||
|
C |
C |
A |
A |
A |
B |
D |
C |
D |
B |
D |
B |
B |
A |
17、(12分)自点A
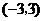 发出的光线
发出的光线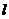 射到
射到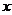 轴上,被
轴上,被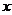 轴反射,其反射光线所在直线与圆
轴反射,其反射光线所在直线与圆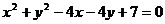 相切,求光线
相切,求光线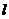 所在的方程。
所在的方程。
18.(12分)(理)过椭圆
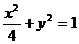 的右焦点F作一直线L交椭圆于A、B两点,且A、B到直线
的右焦点F作一直线L交椭圆于A、B两点,且A、B到直线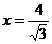 的距离之和为
的距离之和为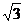 ,求直线L的方程。
,求直线L的方程。
(文)要将两种大小不同的钢板截成A、B、C三种规格的小钢板,其中第一种钢板一张可截成A规格的两块,B规格的一块,C规格的一块,第二种钢板一张可截成A规格的一块,B规格的两块,C规格的三块,今需A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需三种规格的成品,且使所用钢板张数最少。
19.(12分)已知双曲线C1与椭圆C2:
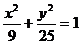 共焦点F1 、F2,它们的离心率之和为
共焦点F1 、F2,它们的离心率之和为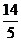 ,
,
(1)求双曲线C1的方程.;
(2)椭圆C2中过点M(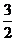 ,
,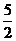 )的弦被点M平分,求这条弦所在直线的一个方向向量;
)的弦被点M平分,求这条弦所在直线的一个方向向量;
20.(12分)已知圆C1:
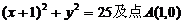 ,Q为圆上一点,AQ的垂直平分线交C1Q于M,
,Q为圆上一点,AQ的垂直平分线交C1Q于M,
(1)求点M的轨迹C2的方程。
(2)曲线C2的一个焦点为F1,对应的准线为l,另一个焦点为F2,问在C2上是否存在点P,使|PF1|是P到l的距离与|PF2|的比例中项?若存在,试求P点的坐标,若不存在,说明理由。
 21.(13分)(理)已知椭圆C:
21.(13分)(理)已知椭圆C: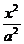 +
+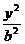 =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=e
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=e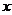 +a与
+a与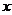 轴.
轴.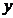 轴分别交于点
轴分别交于点
A、B,M是直线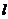 与椭圆C的一个公共点,P是点F1关于直线
与椭圆C的一个公共点,P是点F1关于直线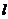 的对称点,设
的对称点,设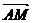 =λ
=λ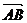 .
.
(1)证明:λ=1-e2;
(2)确定λ的值,使得△PF1F2是等腰三角形.
(文)过椭圆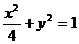 的右焦点F作一直线l交椭圆于A、B两点,且A、B到直线
的右焦点F作一直线l交椭圆于A、B两点,且A、B到直线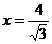 的距离之和为
的距离之和为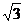 ,求直线L的方程。
,求直线L的方程。

22.( 13分)若F1 、F2为双曲线
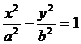 的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
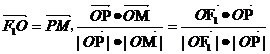
(1)求此双曲线的离心率
(2)若此双曲线过点N(2,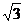 ),求双曲线的方程;
),求双曲线的方程;
(3)设(2)中双曲线的虚轴端点为B1、B2(B1在y轴的正半轴上)过B2作直线l与双曲线交于A、B两点,当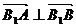 时,求直线l的方程。
时,求直线l的方程。
2007年11月高2009级第三期期中数学试题
命题人:王瑶
16.设P是直线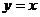 上的点,若椭圆以F1(1,0)F2(2,0)为两个焦点且过P点,则当椭圆的长轴长最短时,它的短轴长2
上的点,若椭圆以F1(1,0)F2(2,0)为两个焦点且过P点,则当椭圆的长轴长最短时,它的短轴长2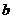 =
.
=
.
15、已知曲线C: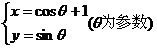 ,点A
,点A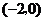 及点B
及点B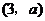 ,从点A观察点B,要使视线不被曲线C挡住,则
,从点A观察点B,要使视线不被曲线C挡住,则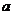 的取值范围是
.
的取值范围是
.
14.渐近线是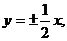 且过点(1,3)的双曲线方程是
.
且过点(1,3)的双曲线方程是
.
13.以椭圆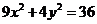 的长轴端点为短轴端点,且过点
的长轴端点为短轴端点,且过点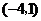 的椭圆标准方程是
的椭圆标准方程是
.
12.(理)已知椭圆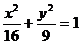 的左、右焦点分别为F1,F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到
的左、右焦点分别为F1,F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到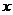 轴的距离为 (
)
轴的距离为 (
)
A.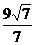 B.
B.
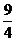 C
.
C
.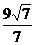 或
或 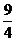 D
.
D
.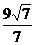 或
或 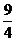 或
或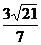
(文)已知椭圆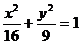 的左、右焦点分别为F1,F2,点P在椭圆上
的左、右焦点分别为F1,F2,点P在椭圆上 ,则点P到
,则点P到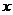 轴的距离为 ( )
轴的距离为 ( )
A.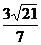 B.
B.
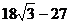 C
.
C
.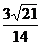 D
.
D
.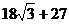

命题人:王瑶
10.设椭圆的两个焦点分别为F1、、F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是 ( )
(A)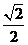 (B)
(B)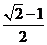 (C)
(C)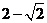 (D)
(D)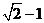
|
|
|

 11.如右图,椭圆
11.如右图,椭圆 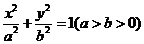 的离心率
的离心率 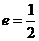 ,
,
|
交于D,
|
|
|
 则
则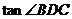 的值等于
( )
的值等于
( )
|
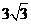 B.
B.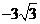 C.
C.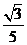 D.
D.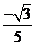
9.设圆过双曲线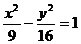 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为:
( )
的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为:
( )
A. 4
B.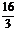 C.
C. 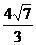 D.5
D.5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com