
6.设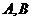 为两个事件,且
为两个事件,且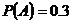 ,则当( )时一定有
,则当( )时一定有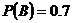
A.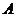 与
与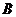 互斥 B.
互斥 B.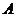 与
与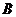 对立 C.
对立 C.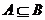 D.
D. 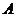 不包含
不包含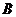
5.先后抛掷骰子三次,则至少一次正面朝上的概率是( )
A.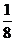 B.
B.
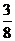 C.
C. 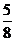 D.
D. 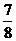
4.在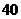 根纤维中,有
根纤维中,有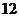 根的长度超过
根的长度超过 ,从中任取一根,取到长度超过
,从中任取一根,取到长度超过 的纤维的概率是( )
的纤维的概率是( )
A.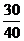 B.
B.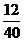 C.
C.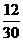 D.以上都不对
D.以上都不对
3.从装有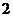 个红球和
个红球和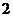 个黒球的口袋内任取
个黒球的口袋内任取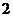 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
A.至少有一个黒球与都是黒球 B.至少有一个黒球与都是黒球
C.至少有一个黒球与至少有 个红球 D.恰有
个红球 D.恰有 个黒球与恰有
个黒球与恰有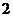 个黒球
个黒球
2.口袋内装有一些大小相同的红球、白球和黒球,从中摸出 个球,摸出红球的概率是
个球,摸出红球的概率是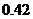 ,摸出白球的概率是
,摸出白球的概率是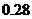 ,那么摸出黒球的概率是( )
,那么摸出黒球的概率是( )
A.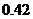 B.
B.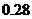 C.
C.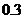 D.
D.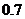
1.同时向上抛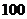 个铜板,落地时
个铜板,落地时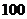 个铜板朝上的面都相同,你认为对这
个铜板朝上的面都相同,你认为对这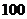 个铜板下面情况更可能正确的是( )
个铜板下面情况更可能正确的是( )
A.这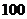 个铜板两面是一样的
个铜板两面是一样的
B.这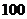 个铜板两面是不同的
个铜板两面是不同的
C.这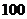 个铜板中有
个铜板中有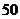 个两面是一样的,另外
个两面是一样的,另外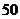 个两面是不相同的
个两面是不相同的
D.这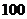 个铜板中有
个铜板中有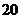 个两面是一样的,另外
个两面是一样的,另外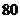 个两面是不相同的
个两面是不相同的
4.一个路口的红绿灯,红灯的时间为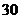 秒,黄灯的时间为
秒,黄灯的时间为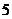 秒,绿灯的时间为
秒,绿灯的时间为
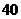 秒,当你到达路口时看见下列三种情况的概率各是多少?
秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3) 不是红灯
新课程高中数学训练题组(咨询13976611338)
(数学3必修)第三章:概率
[综合训练B组]
3.某路公共汽车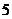 分钟一班准时到达某车站,求任一人在该车站等车时间
分钟一班准时到达某车站,求任一人在该车站等车时间
少于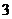 分钟的概率(假定车到来后每人都能上).
分钟的概率(假定车到来后每人都能上).
2.现有一批产品共有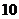 件,其中
件,其中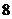 件为正品,
件为正品,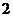 件为次品:
件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续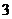 次取出的都是正品的概率;
次取出的都是正品的概率;
(2)如果从中一次取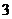 件,求
件,求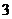 件都是正品的概率.
件都是正品的概率.
1.从甲、乙、丙、丁四个人中选两名代表,求:
(1)甲被选中的概率
(2)丁没被选中的概率
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com