
1.每天/都是一首诗/每个字都是一颗星/像蜜蜂在心头颤动
美好的生活就像诗一样的美,每一个人都希望每天把自己幸福、快乐的人生谱写下来,这种愿望就像星星一样的明亮,像像蜜蜂一样酿造出来蜜一样的甜。
变奏曲:运用变奏手法谱写的乐曲。
凝望:目不转睛地看;注目远望。
朦胧:不清楚,模糊。
颤动(chàn) 僵硬(jiānɡ yìnɡ)
瘦小(shòu) 萤火虫(yíng)
4、某人有4把钥匙,其中2把能打开门。现随机地取1把钥匙试着开门,不能开门的就扔掉,问第二次才能打开门的概率是多少?,若试过的钥匙不扔掉,这个概率又是多少?
3、 从1,2,3,…,9这9个数字中任取2个数字,
(1)2个数字都是奇数的概率为_________;
(2)2个数字之和为偶数的概率为_________.
2、 在20瓶饮料中,有2瓶已过了保质期,从中任取1瓶,取到已过保质期的饮料的概率为_________.
1、一枚硬币连掷3次,只有一次出现正面的概率为_________.
4、总结提高
(1)本节课学习的主要内容是什么?
(2)在应用古典概型解决概率问题时,应注意什么?
(3)学习了古典概型后,你觉得有哪些收获?
3、应用举例
例2 单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案,请大家完成:
Throw two coins of the same quality with both appearing frontage to face ,the probability is ( )
(A)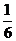 (B)
(B)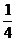 (C)
(C)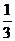 (D)
(D)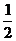
设计意图:先统计全班学生选择A、B、C、D的人数(统计思想),再由学生判断该概率模型(只针对选择A、B、C、D)是不是古典概型,并发现:如果掌握了考察的内容,他可以选择唯一正确的答案;如果掌握了考察的部分内容,他可以提高选择的正确率;假设考生不会做,他只能随机选择一个答案(如某人没有学过英语,他只能猜),答对的概率最低(此时为古典概型),通过亲身感受使学生进一步体验统计与古典概型的意义,同时让学生充分认识到掌握知识的重要性。
探究:在物理考试中既有单选题又有多选题,多选题是从A,B,C,D四个选项中选出所有正确的答案,同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?
设计意图:使学生通过相似问题背景的比较,进一步理解古典概型在解决概率问题中有关的思想方法。
师生活动:主要解决基本事件的个数,这里可以结合例1的结果。
问题3 抛掷一枚质地均匀的骰子,由骰子的点数为奇数还是偶数来决定乒乓球比赛中的发球权,公平吗?同时抛掷两枚质地均匀的骰子,由两枚骰子的点数之和为奇数还是偶数来决定乒乓球比赛中的发球权,公平吗?
设计意图:通过动手操作并利用统计手段(统计思想),使学生深入理解在使用古典概型的概率公式时,首先要正确认识试验中的基本事件(相对于研究问题而言),并判断该概率模型是不是古典概型,然后要找出随机事件A包含的基本事件的个数和试验中基本事件的总数。
师生活动:向每位学生分发一枚质地均匀的骰子,同桌合作做试验,结合试验中的统计数据,通过交流与讨论,尝试解决此问题。在分析此问题时,要引导学生充分认识到:解决同一问题可能有多个角度确定基本事件,但并不是都等可能,只有当它们符合古典概型时,才能运用概率计算公式。
例3 假设某人的储蓄卡的密码是由6个数字组成(每个数字可以是0,1,2,…,9中的任意一个),如果他完全忘记了密码,问他到自动取款机上随机试一次密码就能取到钱的概率是多少?若他知道最后两个数字是自己的生日,结果又会怎样呢?
设计意图:使学生能将实际问题转化(化归思想)为古典概型,了解概率在实际中的应用及其中的化归思想。
练习 某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽出2听,检测到不合格产品的概率有多大?
设计意图:继续培养与提高学生能将实际问题转化为古典概型的能力,不断了解概率在实际中的广泛应用。
探究 随着检测听数的增加,查出不合格产品的概率怎样变化?为什么质检人员一般都采用抽查的方式而不采用逐个检查的方法?
2、归纳公式
问题2 我们知道:抛掷一枚质地均匀的硬币出现正面朝上的概率为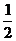 ,抛掷一枚质地均匀的骰子出现“1点”的概率为
,抛掷一枚质地均匀的骰子出现“1点”的概率为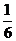 ,由此能否得出古典概型中任何事件的概率计算公式?
,由此能否得出古典概型中任何事件的概率计算公式?
设计意图:使学生从特殊问题入手(借助图形),归纳出古典概型概率计算公式。
师生活动:引导学生从特殊试验中发现任意两个基本事件都是互斥且等可能,从而可以得出任一基本事件的概率,又因为任何事件(包括必然事件)都可以表示为基本事件的和,利用概率的加法公式可以得出结果,并从中体会从特殊到一般归纳问题的思想。
古典概型计算任何事件A的概率计算公式为:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com