
2、AB ⊥OC,AB⊥OD且AC 与PA相交,,所以
AB⊥ 平面ODC,所以得证。
21(1)
、连接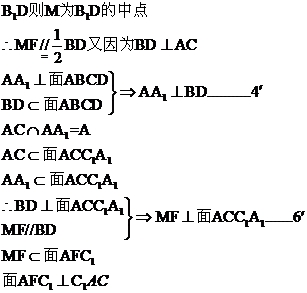
(2)
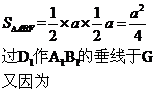
∠BAD=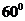
∠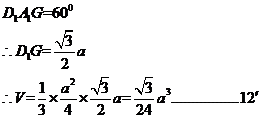
20、解:1、取AB的中点为O,连结DO 、CO,
则∠DOC是其二面角的平面角且是直角
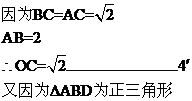
OD=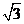
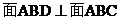
∠DOC是直角
OC=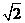 ,则得DC=
,则得DC=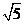 ………………………………….
………………………………….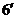
17、 证明:连结A1C1交于B1D1于O1点,
连结AO1
……………………………………… 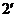
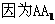
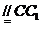 …………………………………………….
…………………………………………….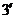

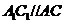 又因为
又因为
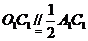
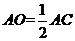
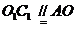
则四边形AO1C1O平行四边形,………………………………………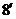
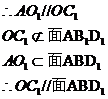 …………………………………………………………
…………………………………………………………
18证明: ……………………………
……………………………
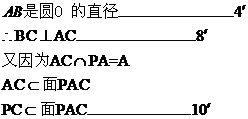
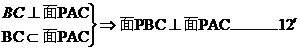
19
解:设棱长为a
取AC中点M链接EM.MF
因为M,E,F分别为AC,SC,AS中点
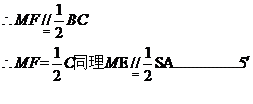
∠MEF是异面直线EF与SA所成的角其补角…………………………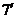
连接SF 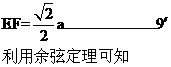
∠MEF=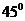 ……………………………………………………
……………………………………………………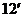
16. 3.4
15. ②⑤
14. 1/3
13. 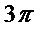 .
.
22、(本题满分14分)
如图,在四棱锥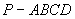 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱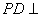 底面
底面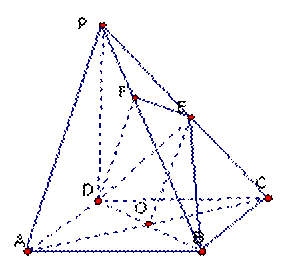 ABCD,
ABCD,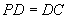 ,E是PC的中点,作
,E是PC的中点,作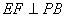 交PB于点F。
(I)证明
交PB于点F。
(I)证明 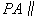 平面
平面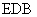 ;
(II)证明
;
(II)证明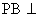 平面EFD;
(III)求二面角
平面EFD;
(III)求二面角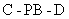 的大小。
的大小。
21.(12分)如图,已知四棱柱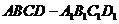 的棱长都为
的棱长都为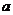 ,底面
,底面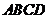 是菱形,且
是菱形,且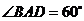 ,侧棱
,侧棱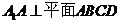 ,
,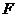 为棱
为棱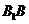 的中点,
的中点,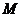 为线段
为线段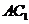 的中点.
的中点.
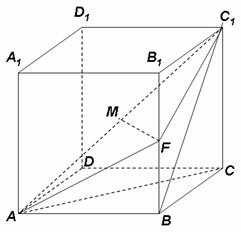 (Ⅰ)求证:平面
(Ⅰ)求证:平面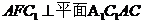 ;
;
(Ⅱ)求三棱锥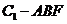 的体积.
的体积.
20. (12分)如图,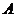 ,
,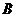 ,
,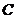 ,
,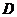 为空间四点,且
为空间四点,且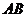
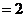 ,
,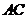
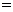
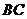
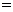
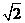 .等边三角形
.等边三角形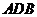 以
以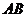 为轴转动.
为轴转动.
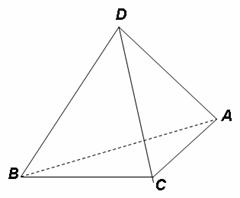 (Ⅰ)当平面
(Ⅰ)当平面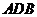
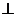 平面
平面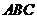 时,求
时,求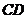 ;
;
(Ⅱ)当△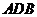 转动时,是否总有
转动时,是否总有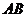
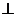
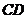 ?证明你的结论.
?证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com