22．(本题12分)如图所示，点(p>0)，点P为抛物线C：²＝2px上的动点，

P到y轴的距离|PN|满足|PF|=|PN|+ 2(1)，直线l过点F，

与抛物线C交于A、B两点.

(1)求抛物线C的方程；

(2)设点(a<0 )，若直线l垂直x轴且

向量的夹角为，求a的值；

(3)设M为线段AB的中点，求点M到直线y=x+1距离的最小值．

21．(本题12分)设函数是定义在[-3，3]上的偶函数，且时， (aÎR)。

　　　 (1)求函数的解析式；

　　　 (2)若函数在上单调递减，求实数a的取值范围；

　　　 (3)当a=6时，求函数的最小值，并求出取到最小值所对应的x值．

20、(本小题满分12分)

如图：直三棱柱ABC-中，，

，D为AB中点。

(1)求证：；

(2)求证：∥平面；

19．(本题12分)已知等差数列{}中=-20，，

　　　　 (1) 求数列{}的通项公式；

(2)若数列{}满足，设，试问：当n取何值时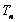=1。

18．(本题12分)已知向量=(cosx, y) ，=(sinx+cosx , -1) (x,yR) 且 ·=0。

(1)求y与x的函数关系y=f(x)的表达式；

(2)当x[0 , ]时,求满足f(x)=1的x值。

17．(本题10分)解关于的不等式