
18. (丰台·理·题17)
某工厂师徒二人各加工相同型号的零件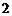 个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为
个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为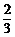 ,师徒二人各加工
,师徒二人各加工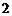 个零件都是精品的概率为
个零件都是精品的概率为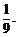
⑴求徒弟加工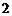 个零件都是精品的概率;
个零件都是精品的概率;
⑵求徒弟加工该零件的精品数多于师父的概率;
⑶设师徒二人加工出的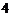 个零件中精品个数为
个零件中精品个数为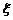 ,求
,求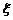 的分布列与均值
的分布列与均值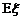 .
.
[解析]
⑴设徒弟加工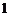 个零件是精品的概率为
个零件是精品的概率为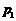 ,则
,则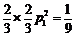 ,得
,得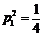 ,
,
所以徒弟加工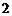 个零件都是精品的概率是
个零件都是精品的概率是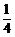
⑵设徒弟加工零件的精品数多于师父的概率为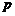 ,
,
由⑴知,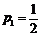 ,师父加工两个零件中,精品个数的分布列如下:
,师父加工两个零件中,精品个数的分布列如下:
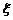 |
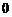 |
1 |
2 |
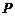 |
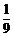 |
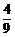 |
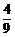 |
徒弟加工两个零件中,精品个数的分布列如下:
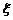 |
0 |
1 |
2 |
|
P |
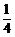 |
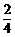 |
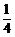 |
所以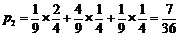
⑶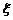 的分布列为
的分布列为
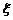 |
0 |
1 |
2 |
3 |
4 |
|
P |
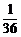 |
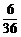 |
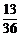 |
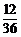 |
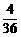 |
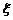 的期望为
的期望为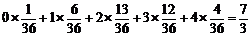 .
.
17. (丰台·文·题17)
某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.


⑴求全班人数及分数在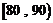 之间的频数;
之间的频数;
⑵估计该班的平均分数,并计算频率分布直方图中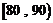 间的矩形的高;
间的矩形的高;
⑶若要从分数在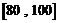 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在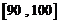 之
之 间的概率.
间的概率.
[解析]
⑴由茎叶图知,分数在 之间的频数为
之间的频数为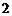 ,频率为
,频率为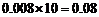 ,
,
全班人数为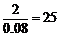 .
.
所以分数在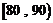 之间的频数为
之间的频数为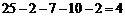
⑵分数在 之间的总分为
之间的总分为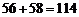 ;
;
分数在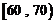 之间的总分为
之间的总分为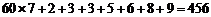 ;
;
分数在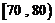 之间的总分数为
之间的总分数为
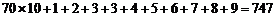 ;
;
分数在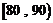 之间的总分约为
之间的总分约为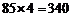 ;
;
分数在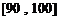 之间的总分数为
之间的总分数为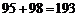 ;
;
所以,该班的平均分数为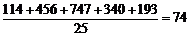 .
.
估计平均分时,以下解法也给分:
分数在 之间的频率为
之间的频率为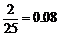 ;
;
分数在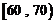 之间的频率为
之间的频率为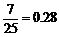 ;
;
分数在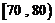 之间的频率为
之间的频率为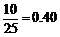 ;
;
分数在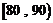 之间的频率为
之间的频率为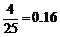 ;
;
分数在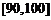 之间的频率为
之间的频率为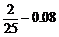 ;
;
所以,该班的平均分约为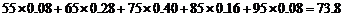
频率分布直方图中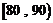 间的矩形的高为
间的矩形的高为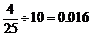 .
.
⑶将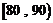 之间的
之间的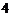 个分数编号为
个分数编号为 ,
,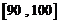 之间的
之间的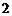 个分数编号为
个分数编号为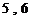 ,在
,在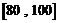 之间的试卷中任取两份的基本事件为:
之间的试卷中任取两份的基本事件为:
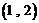 ,
,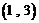 ,
,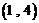 ,
,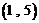 ,
,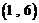
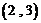 ,
,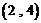 ,
,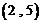 ,
,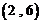 ,
,
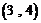 ,
,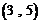 ,
,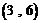
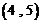 ,
,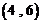
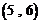 共
共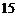 个,
个,
其中,至少有一个在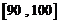 之间的基本事件有
之间的基本事件有 个,
个,
故至少有一份分数在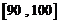 之间的概率是
之间的概率是 .
.
16. (朝阳·理·题16)
在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮.现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是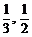 .两人投篮3次,且第一次由甲开始投篮,假设每人每次投篮命中与否均互不影响.
.两人投篮3次,且第一次由甲开始投篮,假设每人每次投篮命中与否均互不影响.
⑴求3次投篮的人依次是甲、甲、乙的概率;
⑵若投篮命中一次得1分,否则得0分,用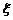 表示甲的总得分,求
表示甲的总得分,求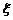 的分布列和数学期望.
的分布列和数学期望.
[解析]
⑴记“3次投篮的人依次是甲、甲、乙”为事件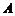 .
.
由题意,得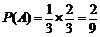
答:3次投篮的人依次是甲、甲、乙的概率是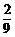 .
.
⑵由题意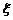 的
的 可能有取值为0,1,2,3,则
可能有取值为0,1,2,3,则
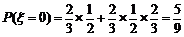 ,
,
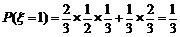 .
.
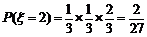 ,
,
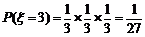 .
.
所以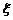 的分布列为
的分布列为
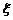 |
0 |
1 |
2 |
3 |
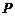 |
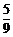 |
 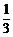 |
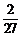 |
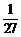 |
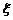 的数学期望
的数学期望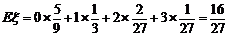 .
.
15. (朝阳·文·题16)
袋子中装有编号为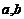 的2个黑球和编号为
的2个黑球和编号为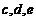 的3个红球,从中任意摸出2个球.
的3个红球,从中任意摸出2个球.
⑴写出所有不同的结果;
⑵求恰好摸出1个黑球和1个红球的概率;
⑶求至少摸出1个黑球的概率.
[解析]
⑴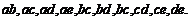 3分
3分
⑵记“恰好摸出1个黑球和1个红球”为事件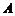 ,
,
则事件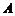 对应的基本事件为
对应的基本事件为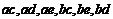 ,共6个基本事件,所以
,共6个基本事件,所以
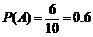 …..8分
…..8分
答:恰好摸出1个黑球和1个红球的概率为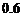
⑶记“至少摸 出1个黑球”为事件
出1个黑球”为事件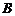 ,
,
则事件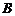 包含的基本事件为
包含的基本事件为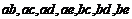 ,共7个基本事件,
,共7个基本事件,
所以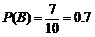
答:至少摸出1个黑 球的概率为
球的概率为 …..13分
…..13分
14. (崇文·文·题16)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了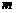 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为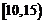 ,
,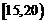 ,
,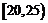 ,
,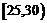 ,
,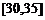 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在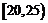 之间的工人有6位.
之间的工人有6位.
⑴求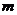 ;
;
⑵工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
人不在同一组的概率是多少?
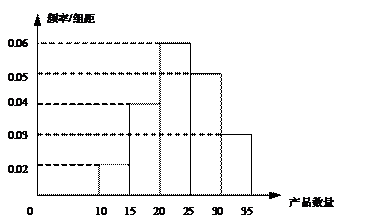
[解析]
⑴根据直方图可知产品件数在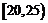 内的人数为
内的人数为
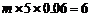 ,则
,则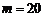 (位).
(位).
⑵根据直方图可知产品件数在 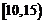 ,
,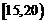 ,组内的人数分别为2,4.
,组内的人数分别为2,4.
设这2位工人不在同一组为A事件,则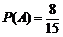 .
.
答:选取这2人不在同组的概率为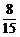 .
.
13. (崇文·文·题11)
从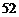 张扑克牌(没有大小王)中随机的抽一张牌,这张牌是
张扑克牌(没有大小王)中随机的抽一张牌,这张牌是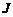 或
或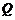 或
或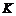 的概率为_______.
的概率为_______.
[解析]
 ;
;
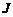 或
或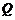 或
或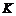 的牌一共12张.于是抽到这三张牌的概率为
的牌一共12张.于是抽到这三张牌的概率为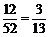 .
.
12. (崇文·理·题16)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了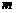 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为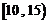 ,
,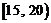 ,
,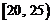 ,
, ,
,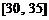 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在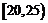 之间的工人有6位.
之间的工人有6位.
⑴求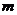 ;
;
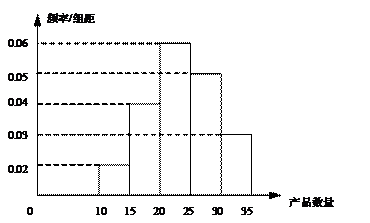
⑵工厂规定从各组中任选1人进行再培训,则选取5人不在同一组的概率是多少?
[解析]
⑴根据直方图可知产品件数在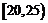 内的人数为
内的人数为
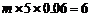 ,则
,则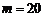 (位).
(位).
⑵根据直方图可知产品件数在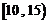 ,
,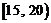 ,
,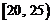 ,
, ,
,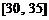 ,
,
组内的人数分别为2,4,6, 5,3.
设选取这5人不在同组为B事件,则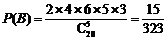 .
.
答:选取这5人不在同组的概率为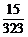 .
.
11. (东城·文·题16)
在一次数学统考后,某班随机抽取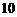 名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.
名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.
⑴计算样本的平均成绩及方差;
⑵在这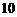 个样本中,现从不低于
个样本中,现从不低于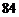 分的成绩中随机抽取
分的成绩中随机抽取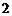 个,求
个,求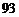 分的成绩被抽中的概率.
分的成绩被抽中的概率.
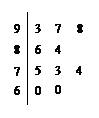
[解析]
⑴样本的平均成绩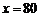 .
.
样本方差为

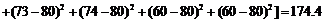 ,
,
⑵设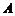 表示随机事件“
表示随机事件“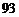 分的成绩被抽中”,从不低于
分的成绩被抽中”,从不低于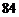 分的成绩中随机抽取
分的成绩中随机抽取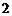 个的样本总数是:
个的样本总数是: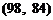 ,
,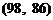 ,
,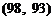 ,
,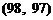 ,
, ,
,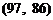 ,
, ,
,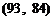 ,
,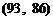 ,
,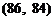 共
共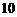 种.
种.
而事件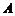 含有
含有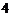 个基本事件:
个基本事件: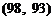 ,
, ,
,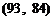 ,
,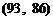 .
.
所以所求概率为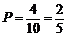 .
.
10. (西城·理·题16)
在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问题,能正确回答者 进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为
进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为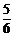 、
、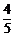 、
、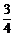 、
、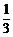 ,且各
,且各 轮问题能否正确回答互不影响.
轮问题能否正确回答互不影响.
⑴求该选手进入第三轮才被淘汰的概率;
⑵求该选手至多进入第三轮考核的概率;
⑶该选手在选拔过程中回答过的问题的个数记为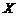 ,求随机变量
,求随机变量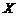 的分布列和期望.
的分布列和期望.
[解析]
设事件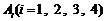 表示“该选手能正确回答第
表示“该选手能正确回答第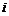 轮问题”,
轮问题”,
由已知 ,
,
⑴设事件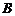 表示“该选手进入第三轮被淘汰”,
表示“该选手进入第三轮被淘汰”,
则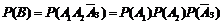
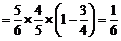 .
.
⑵设事件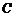 表示“该选手至多进入第三轮考核”,
表示“该选手至多进入第三轮考核”,
则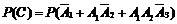
 ;
;
⑶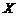 的可能取值为1,2,3,4,
的可能取值为1,2,3,4,
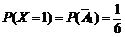 ,
,
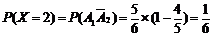 ,
,
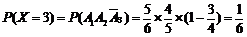 ,
,
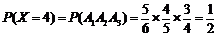 ,
,
所以,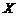 的分布列为
的分布列为
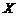 |
1 |
2 |
3 |
4 |
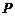 |
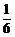 |
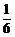 |
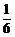 |
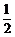 |
 .
.
9. (石景山·文·题16)
为援助汶川灾后重建,对某项工程进行竞标,共有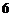 家企业参与竞标.其中
家企业参与竞标.其中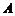 企业来自辽宁省,
企业来自辽宁省,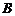 、
、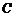 两家企业来自福建省,
两家企业来自福建省, 、
、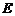 、
、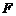 三家企业来自河南省.此项工程需要两家企业联合施工,假设每家企业中标的概率相同.
三家企业来自河南省.此项工程需要两家企业联合施工,假设每家企业中标的概率相同.
⑴企业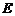 中标的概率是多少?
中标的概率是多少?
⑵在中标的企业中,至少有一家来自河南省的概率是多少?
[解析]
⑴从这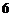 家企业中选出
家企业中选出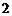 家的选法有
家的选法有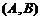 ,
, ,
,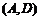 ,
,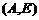 ,
,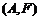 ,
,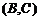 ,
,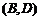 ,
, ,
,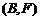 ,
,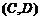 ,
,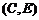 ,
,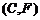 ,
,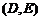 ,
, ,
,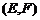 ,共有
,共有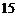 种.
种.
其中企业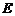 中标的选法有
中标的选法有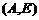 ,
, ,
,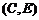 ,
,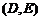 ,
,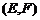 ,共
,共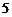 种,
种,
则企业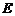 中标的概率为
中标的概率为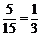 .
.
⑵解法一:在中标的企业中,至少有一家来自河南省选法有
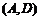 ,
,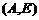 ,
,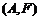 ,
,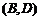 ,
, ,
,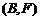 ,
,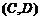 ,
,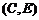 ,
,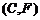 ,
,
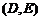 ,
, ,
,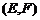 ,共
,共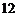 种.
种.
则“在中标的企业中,至少有一家来自河南省”的概率为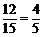 .
.
解法二:在中标的企业中,没有来自河南省选法有: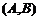 ,
, ,
,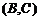 ,共
,共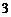 种.
种.
∴“在中标的企业中,没有来自河南省”概率为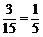 .
.
∴“在中标的企业中,至少有一家来自河南省”的概率为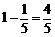 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com