
15. (丰台·文·题12)
函数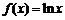 的图象在点
的图象在点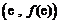 处的切线方程是
.
处的切线方程是
.
[解析]
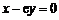 ;
;
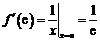 ,∴所求的切线方程为
,∴所求的切线方程为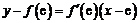 ,
,
即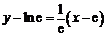 ,化简为
,化简为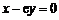 .
.
14. (石景山·文·题9)
函数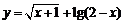 的定义域是
.
的定义域是
.
[解析]
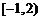 ;
;
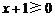 且
且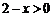
13. (宣武·理·题8)
设函数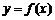 的定义域为
的定义域为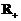 ,若对于给定的正数
,若对于给定的正数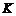 ,定义函数
,定义函数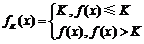 , 则当函数
, 则当函数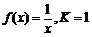 时,定积分
时,定积分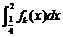 的值为( )
的值为( )
A.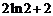 B.
B.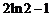 C.
C.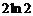 D.
D.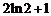
[解析] D;
由题设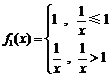 ,于是定积分
,于是定积分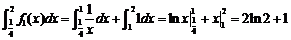 .
.
12. (东城·理·题8)
定义在 上的函数
上的函数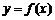 是减函数,且函数
是减函数,且函数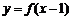 的图象关于
的图象关于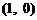 成中心对称,若
成中心对称,若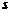 ,
,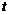 满足不等式
满足不等式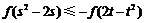 .则当
.则当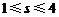 时,
时, 的取值范围是( )
的取值范围是( )
A.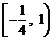 B.
B.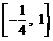 C.
C.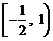 D.
D.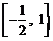
[解析] D;
由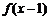 的图象关于
的图象关于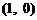 中心对称知
中心对称知 的图象关于
的图象关于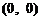 中心对称,故
中心对称,故 为奇函数得
为奇函数得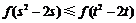 ,从而
,从而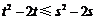 ,化简得
,化简得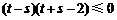 ,又
,又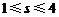 ,故
,故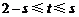 ,从而
,从而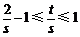 ,等号可以取到,而
,等号可以取到,而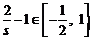 ,故
,故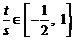 .
.
11. (东城·文·题8)
已知函数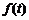 是奇函数且是
是奇函数且是 上的增函数,若
上的增函数,若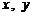 满足不等式
满足不等式 ,则
,则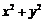 的最大值是( )
的最大值是( )
A.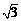 B.
B.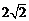 C.
C.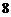 D.
D.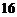
[解析] C;
由 为奇函数得
为奇函数得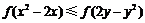 ,又
,又 为增函数,有
为增函数,有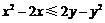 ,即
,即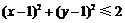 ,它表示圆心在
,它表示圆心在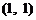 ,半径为
,半径为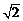 的圆的内部(包括边界),故到原点最远的点为
的圆的内部(包括边界),故到原点最远的点为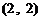 ,从而
,从而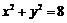 .
.
10. (石景山·理·题8)(石景山·文·题8)
已知函数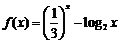 ,正实数
,正实数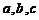 是公差为正数的等差数列,且满足
是公差为正数的等差数列,且满足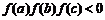 .若实数
.若实数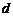 是方程
是方程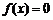 的一个解,那么下列四个判断:
的一个解,那么下列四个判断:
①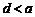 ;②
;②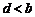 ;③
;③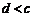 ;④
;④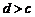 中有可能成立的个数为( )
中有可能成立的个数为( )
A.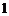 B.
B.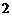 C.
C.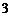 D.
D.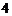
[解析] C;
 在
在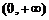 上单调减,值域为
上单调减,值域为 .又
.又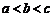 ,
,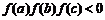 ,所以
,所以
⑴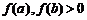 ,
,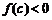 .由
.由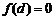 可知,
可知,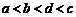 ,③成立;
,③成立;
⑵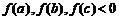 .此时
.此时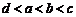 ,①②③成立.
,①②③成立.
综上,可能成立的个数为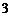 .
.
9. (石景山·理·题7)(石景山·文·题7)
已知函数 的导函数
的导函数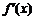 的图象如图所示,那么函数
的图象如图所示,那么函数 的图象最有可能的是( )
的图象最有可能的是( )
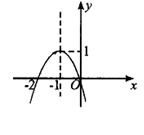
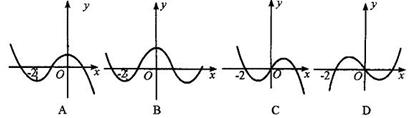
[解析] A;
由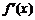 的图象知
的图象知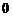 和
和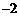 是
是 的极值点,且
的极值点,且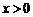 时,
时, 单调递减,故选A.
单调递减,故选A.
8. (宣武·文·题6)
设函数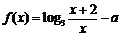 在区间
在区间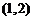 内有零点,则实数
内有零点,则实数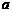 的取值范围是( )
的取值范围是( )
A.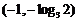 B.
B.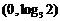 C.
C.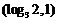 D.
D.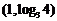
[解析] C;
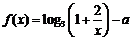 在
在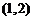 上是减函数,由题设有
上是减函数,由题设有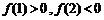 ,得解.
,得解.
7. (海淀·文·题5)
在同一坐标系中画出函数 ,
, ,
, 的图象,可能正确的是( )
的图象,可能正确的是( )

[解析] D;
 在B、C、D三个选项中对应的
在B、C、D三个选项中对应的 ,只有选项D的图象正确.
,只有选项D的图象正确.
6. (丰台·理·题4)(丰台·文·题6)
奇函数 在
在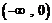 上单调递增,若
上单调递增,若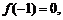 则不等式
则不等式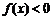 的解集是( )
的解集是( )
A.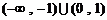
 B.
B.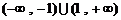
C.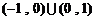 D.
D.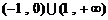
[解析] A;

如图,根据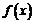 所具有的性质可以画出
所具有的性质可以画出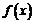 的草图,因此
的草图,因此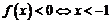 或
或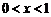 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com