
25. (丰台·理·题18)
已知函数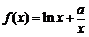 .
.
⑴当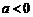 时,求函数
时,求函数 的单调区间;
的单调区间;
⑵若函数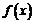 在
在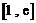 上的最小值是
上的最小值是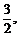 求
求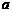 的值.
的值.
[解析]
函数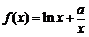 的定义域为
的定义域为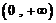 ,
,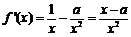
⑴∵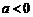 ,∴
,∴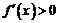
故函数在其定义域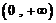 上是单调递增的.
上是单调递增的.
⑵在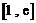 上,发如下情况讨论:
上,发如下情况讨论:
①当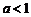 时,
时,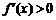 ,函数
,函数 单调递增,其
单调递增,其 最小值为
最小值为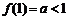 ,
,
这与函数在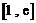 上的最小值是
上的最小值是 相矛盾;
相矛盾;
②当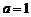 时,函数
时,函数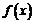 在
在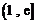 单调递增,其最小值为
单调递增,其最小值为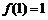 ,同样与最小值是
,同样与最小值是 相矛盾;
相矛盾;
③当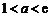 时,函数
时,函数 在
在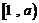
 上有
上有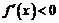 ,单调递减,
,单调递减,
在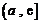 上有
上有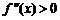 ,单调递增,所以函数
,单调递增,所以函数 满足最小值为
满足最小值为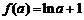
由 ,得
,得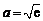 .
.
④当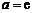 时,函数
时,函数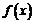 在
在 上有
上有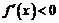 ,单调递减,其最小值为
,单调递减,其最小值为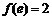 ,还与最小值是
,还与最小值是 相矛盾;
相矛盾;
⑤当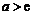 时,显然函数
时,显然函数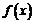 在
在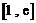 上单调递减,其最小值为
上单调递减,其最小值为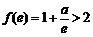 ,
,
仍与最小值是 相矛盾;
相矛盾;
综上所述,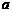 的值为
的值为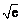 .
.
24. (丰台·文·题18)
设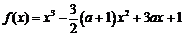 .
.
⑴若函数 在区间
在区间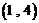 内单调递减,求
内单调递减,求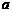 的取值范围;
的取值范围;
⑵若函数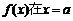 处取得极小值是
处取得极小值是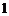 ,求
,求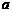 的值,并说明在区间
的值,并说明在区间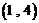 内函数
内函数 的单调性.
的单调性.
[解析]
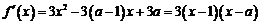
⑴∵函数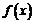 在区间
在区间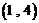 内单调递减,
内单调递减,
∵ ,∴
,∴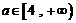 .
.
⑵∵函数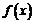 在
在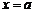 处有极值是
处有极值是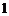 ,∴
,∴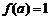 .
.
即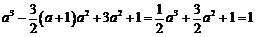 .
.
∴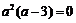 ,所以
,所以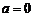 或
或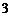 .
.
当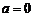 时,
时,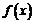 在
在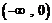 上单调递增,在
上单调递增,在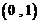 上单调递减,所以
上单调递减,所以 为极大值,
为极大值,
这与函数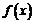 在
在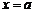 处取得极小值是
处取得极小值是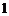 矛盾,
矛盾,
所以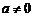 .
.
当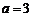 时,
时,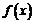 在
在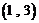 上单调递减,在
上单调递减,在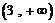 上单调递增,所以
上单调递增,所以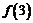 为极小值,
为极小值,
所以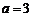 时,此时,在区间
时,此时,在区间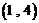 内函数
内函数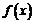 的单调性是:
的单调性是:
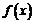 在
在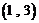 内减,在
内减,在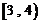 内增.
内增.
23. (宣武·理·题14)
有下列命题:
①若 存在导函数,则
存在导函数,则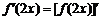 ;
;
②若函数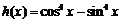 ,则
,则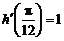 ;
;
③若函数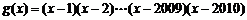 ,则
,则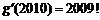 ;
;
④若三次函数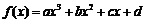 ,则“
,则“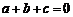 ”是“
”是“ 有极值点”的充要条件.
有极值点”的充要条件.
其中真命题的序号是 .
[解析] ③;
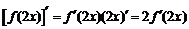 ,①错误;
,①错误;
 ,则
,则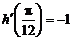 ,②错;
,②错;
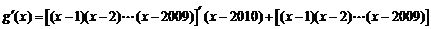 ,③正确;
,③正确;
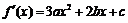 ,
,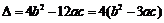 ,只需
,只需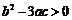 即可,
即可,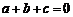 是
是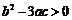 的充分不必要条件.
的充分不必要条件.
22. (宣武·文·题14)
有下列命题:
①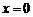 是函数
是函数 的极值点;
的极值点;
②三次函数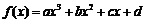 有极值点的充要条件是
有极值点的充要条件是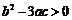 ;
;
③奇函数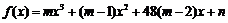 在区间
在区间 上是单调减函数.
上是单调减函数.
其中假命题的序号是 .
[解析] ①;
 在
在 上单调增,没有极值点,①错;
上单调增,没有极值点,①错;
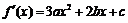 ,
, 有极值点的充要条件是
有极值点的充要条件是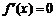 有两个不相等的实根,
有两个不相等的实根,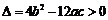 ,也即
,也即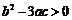 ,②正确;
,②正确;
 是奇函数,则
是奇函数,则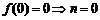 ,由
,由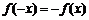 ,可得
,可得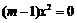 ,因此
,因此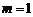 ,所以
,所以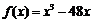 .当
.当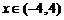 时,
时,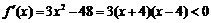 ,故
,故 在
在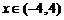 上是单调减函数.
上是单调减函数.
21. (西城·理·题14)
设函数 的定义域为
的定义域为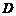 ,若存在非零实数
,若存在非零实数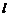 使得对于任意
使得对于任意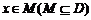 ,有
,有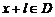 ,且
,且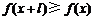 ,则称
,则称 为
为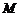 上的
上的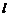 高调函数.
高调函数.
如果定义域为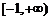 的函数
的函数 为
为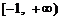 上的
上的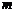 高调函数,那么实数
高调函数,那么实数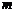 的取值范围是
.
的取值范围是
.
如果定义域为 的函数
的函数 是奇函数,当
是奇函数,当 时,
时,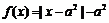 ,且
,且 为
为 上的4高调函数,那么实数
上的4高调函数,那么实数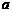 的取值范围是
.
的取值范围是
.
[解析]
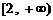 ;
;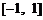 ;
;
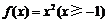 的图象如下图左所示,要使得
的图象如下图左所示,要使得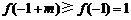 ,有
,有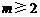 ;
; 时,恒有
时,恒有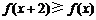 ,故
,故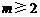 即可;
即可;
由 为奇函数及
为奇函数及 时的解析式知
时的解析式知 的图象如下图右所示,
的图象如下图右所示,
∵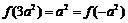 ,由
,由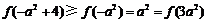 ,故
,故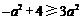 ,从而
,从而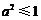 ,又
,又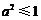 时,恒有
时,恒有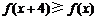 ,故
,故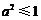 即可.
即可.

20. (西城·文·题14)
设函数 的定义域为
的定义域为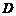 ,若存在非零实数
,若存在非零实数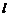 使得对于任意
使得对于任意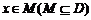 ,有
,有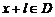 ,且
,且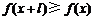 ,则称
,则称 为
为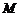 上的
上的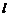 高调函数.
高调函数.
现给出下列命题:
①函数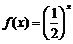 为
为 上的
上的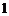 高调函数;
高调函数;
②函数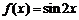 为
为 上的
上的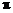
 高调函数;
高调函数;
③如果定义域为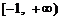 的函数
的函数 为
为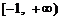 上
上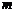 高调函数,那么实数
高调函数,那么实数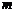 的取值范围是
的取值范围是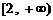 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
[解析] ②③;
①中 为减函数,故不可能是
为减函数,故不可能是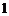 高调函数;②中,
高调函数;②中,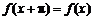 ,故②正确;
,故②正确;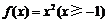 的图象如下图所示,要使得
的图象如下图所示,要使得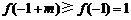 ,有
,有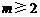 ;
; 时,恒有
时,恒有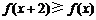 ,故
,故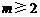 即可,③正确.
即可,③正确.

19. (东城·理·题14)
如果对任意一个三角形,只要它的三边长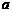 ,
,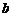 ,
,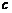 都在函数
都在函数 的定义域内,就有
的定义域内,就有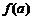 ,
,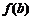 ,
, 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称 为“Л型函数”.则下列函数:
为“Л型函数”.则下列函数:
①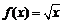 ; ②
; ②
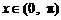 ; ③
; ③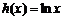
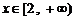 ,
,
是“Л型函数”的序号为 .
[解析] ①③;
若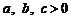 ,
,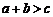 ,则
,则 ,故①满足;若
,故①满足;若 ,
,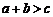 ,则
,则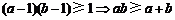 ,
,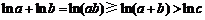 ,故③满足;②反例:
,故③满足;②反例: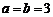 ,
,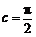 时,
时, 构成三角形,但
构成三角形,但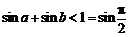 ,故
,故 不构成三角形.
不构成三角形.
18. (丰台·理·题14)
函数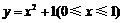 图象上点
图象上点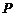 处的切线与直线
处的切线与直线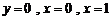 围成的梯形面积等于
围成的梯形面积等于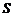 ,则
,则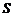 的最大值等于
,此时点
的最大值等于
,此时点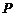 的坐标是
.
的坐标是
.
[解析]
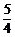 ,
,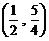 ;
;
函数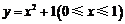 在
在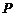
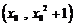 点处的切线方程为
点处的切线方程为
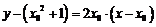 ,即
,即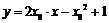
它与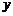 轴的交点为
轴的交点为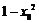 ,与
,与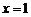 的交点为
的交点为 .
.
于是题中梯形的面积
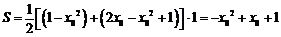
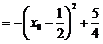
当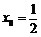 时,
时,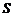 取得最大值为
取得最大值为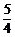 ,
,
此时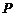 点坐标为
点坐标为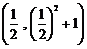 即
即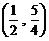 .
.
17. (丰台·文·题13)
已知函数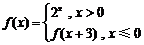 ,
, .
.
[解析]
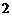 ;
;
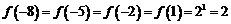 .
.
16. (西城·文·题12)
已知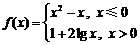 ,若
,若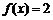 ,则
,则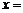 .
.
[解析]
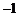 或
或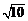 ;
;
当 时,由
时,由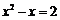 得,
得,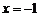 (正值舍);当
(正值舍);当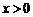 时,
时,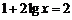 ,解得
,解得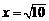 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com