
1、设集合 ,
,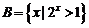 ,则
,则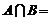 ▲ .
▲ .
20. (本小题满分16分)
数列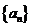 中,
中,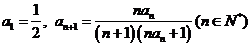 ,其前
,其前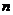 项的和为
项的和为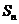 .
.
求证: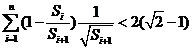 .
.
第4页 (共4页)徐州市高三数学信息卷
19.(本小题满分16分)
公民在就业的第一年就交纳养老储备金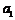 ,以后每年交纳的数目均比上一年增加
,以后每年交纳的数目均比上一年增加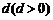 ,历年所交纳的储备金数目
,历年所交纳的储备金数目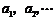 是一个公差为
是一个公差为 的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.如果固定年利率为
的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.如果固定年利率为 ,那么,在第
,那么,在第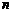 年末,第一年所交纳的储备金就变为
年末,第一年所交纳的储备金就变为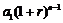 ,第二年所交纳的储备金就变为
,第二年所交纳的储备金就变为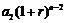 ,
, .以
.以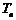 表示到第
表示到第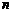 年末所累计的储备金总额.
年末所累计的储备金总额.
求证: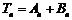 ,其中
,其中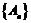 是一个等比数列,
是一个等比数列,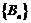 是一个等差数列.
是一个等差数列.
18. (本小题满分14分)
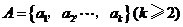 ,其中
,其中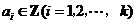 ,由
,由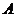 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: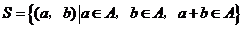 ,
,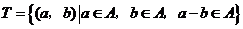 .其中
.其中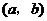 是有序数对,集合
是有序数对,集合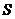 和
和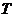 中的元素个数分别为
中的元素个数分别为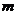 和
和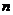 .若对于任意的
.若对于任意的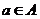 ,总有
,总有 ,则称集合
,则称集合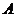 具有性质
具有性质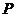 .
.
(I)对任何具有性质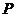 的集合
的集合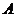 ,证明:
,证明: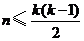 ;
;
(II)判断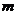 和
和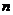 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
17. (本小题满分15分)设常数 ,函数
,函数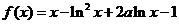
(1)令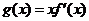
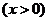 ,求
,求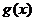 的最小值,并比较
的最小值,并比较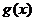 的最小值与0的大小;
的最小值与0的大小;
(2)求证: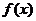 在
在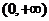 上是增函数;
上是增函数;
(3)求证:当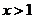 时,恒有
时,恒有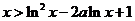 .
.
第3页 (共4页)徐州市高三数学信息卷
16. (本小题满分15分)
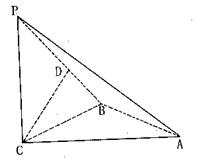 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,
D是PB上一点,且CD⊥平面PAB。
(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小;
15. (本小题满分14分)
已知直线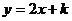 被抛物线
被抛物线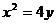 截得的弦长
截得的弦长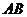 为20,
为20,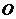 为坐标原点.
为坐标原点.
(1)求实数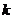 的值;
的值;
(2)问点 位于抛物线弧
位于抛物线弧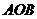 上何处时,△
上何处时,△ 面积最大?
面积最大?
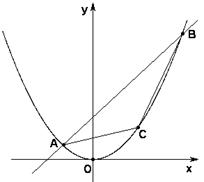
14.已知一组抛物线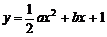 ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是___ ★ ___.
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是___ ★ ___.
13. 已知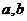 是不相等的两个正数,在
是不相等的两个正数,在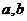 之间插入两组数:
之间插入两组数: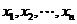 和
和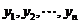 ,(
,( 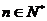 ,且
,且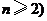 ,使得
,使得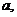
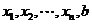 成等差数列,
成等差数列, 成等比数列.老师给出下列五个式子:①
成等比数列.老师给出下列五个式子:①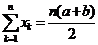 ;②
;②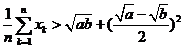 ; ③
; ③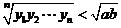 ;④
;④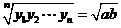 ;⑤
;⑤ .
.
其中一定成立的是___ ★ ___.

第2页 (共4页)徐州市高三数学信息卷
12. 某超市采用“满一百送二十,连环送”的酬宾促销方式,即顾客在店内花钱满100元,就送20元,满200元就送40元奖励劵,满300元就送60元奖励劵….当是有一位顾客共花出现金7020元,如果按照酬宾促销方式,他最多能购买 元的商品。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com