
18. 解:方法二:在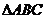 中,由正弦定理得:
中,由正弦定理得: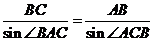 ,
,
∴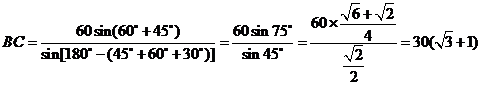 …………6分
…………6分
同理,在在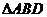 中,由正弦定理得:
中,由正弦定理得: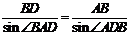
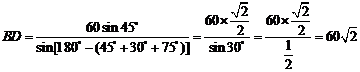 -…………………………10分
-…………………………10分
∴计算出 后,再在
后,再在 中,应用余弦定理计算出
中,应用余弦定理计算出 两点间的距离:
两点间的距离:
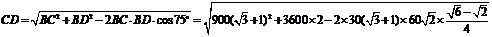 …12分
…12分
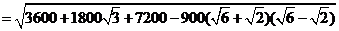
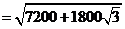
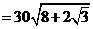
∴ 两艘轮船相距
两艘轮船相距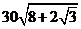
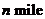 . …………………………………………………15分
. …………………………………………………15分
20、解: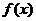 的定义域是(0,+
的定义域是(0,+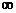 ),
),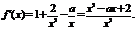
设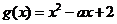 ,二次方程
,二次方程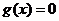 的判别式
的判别式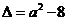 .
.
① 当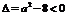 ,即
,即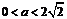 时,对一切
时,对一切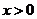 都有
都有 ,此时
,此时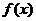 在
在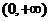 上是增函数。
上是增函数。
② 当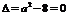 ,即
,即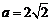 时,仅对
时,仅对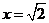 有
有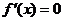 ,对其余的
,对其余的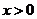 都有
都有 ,此时
,此时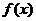 在
在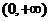 上也是增函数。
上也是增函数。
③ 当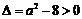 ,即
,即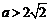 时,方程
时,方程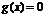 有两个不同的实根
有两个不同的实根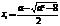 ,
,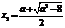 ,
,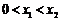 .
.
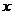 |
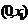 |
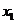 |
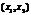 |
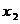 |
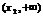 |
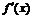 |
+ |
0 |
_ |
0 |
+ |
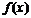 |
单调递增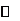 |
极大 |
单调递减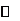 |
极小 |
单调递增 |
此时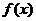 在
在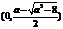 单调递增, 在
单调递增, 在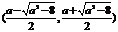 上单调递减, 在
上单调递减, 在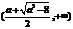 上单调递增.
上单调递增.
19. 解:(Ⅰ)∵抛物线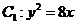 的焦点为
的焦点为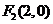 ,
,
∴双曲线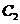 的焦点为
的焦点为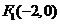 、
、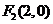 ,
…………… 1分
,
…………… 1分
设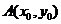 在抛物线
在抛物线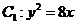 上,且
上,且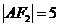 ,
,
由抛物线的定义得,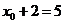 ,∴
,∴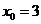 ,
………………………2分
,
………………………2分
∴ ,∴
,∴ ,
………………………… 3分
,
………………………… 3分
∴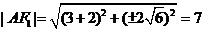 , …………………………………… 4分
, …………………………………… 4分
又∵点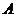 在双曲线上,由双曲线定义得,
在双曲线上,由双曲线定义得,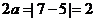 ,∴
,∴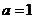 , ………………… 5分
, ………………… 5分
∴双曲线的方程为: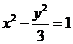 .
……………………… 6分
.
……………………… 6分
(Ⅱ)设圆 的方程为:
的方程为: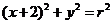 ,双曲线的渐近线方程为:
,双曲线的渐近线方程为: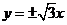 ,
,
∵圆 与渐近线
与渐近线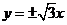 相切,∴圆
相切,∴圆 的半径为
的半径为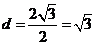 ,……………… 7分
,……………… 7分
故圆 :
: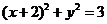 ,
…………………… 8分
,
…………………… 8分
设点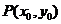 ,则
,则 的方程为
的方程为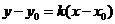 ,即
,即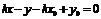 ,
,
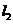 的方程为
的方程为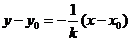 ,即
,即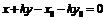 ,
,
∴点 到直线
到直线 的距离为
的距离为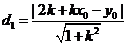 ,点
,点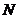 到直线
到直线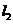 的距离为
的距离为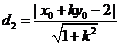 ,
,
∴直线 被圆
被圆 截得的弦长
截得的弦长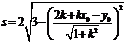 ,
,
直线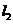 被圆
被圆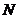 截得的弦长
截得的弦长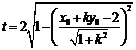 ,
……………………… 11分
,
……………………… 11分
由题意可得,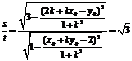 ,即
,即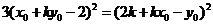 ,
,
∴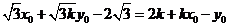 ① 或
① 或 ② 12分
② 12分
由①得: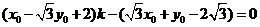 ,
,
∵该方程有无穷多组解,
∴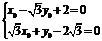 ,解得
,解得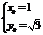 ,点
,点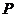 的坐标为
的坐标为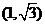 .…………… 14分
.…………… 14分
由②得: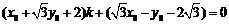 ,
,
∵该方程有无穷多组解,∴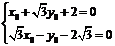 ,解得
,解得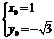 ,点
,点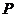 的坐标为
的坐标为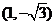 .
.
∴满足条件的点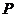 的坐标为
的坐标为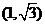 或
或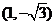 .
………………… 16分
.
………………… 16分
18. 解:在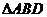 中,由正弦定理得:
中,由正弦定理得: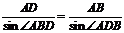 ,
,
∴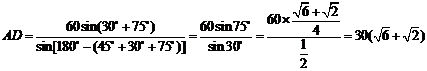 …………4分
…………4分
同理,在在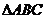 中,由正弦定理得:
中,由正弦定理得:
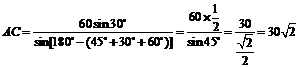 ……………………………………10分
……………………………………10分
∴计算出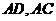 后,再在
后,再在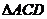 中,应用余弦定理计算出
中,应用余弦定理计算出 两点间的距离:
两点间的距离:
……………………………………12分
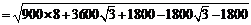
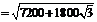
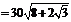
∴ 两艘轮船相距
两艘轮船相距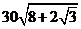
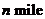 .………………………………………………15分
.………………………………………………15分
17.解:(1)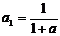 ,
,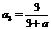 ,
,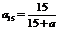 ,
,
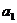 ,
,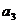 ,
,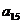 成等比数列,∴
成等比数列,∴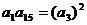 ,∴
,∴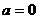 或
或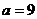 ……5分
……5分
∵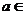
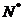 ,∴
,∴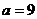 .
……7分
.
……7分
(2) 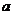 满足条件,
满足条件,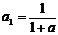 ,
,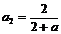 ,
,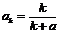 ,
,
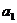 ,
,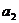 ,
,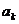 成等差数列,∴
成等差数列,∴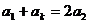 ,化简得
,化简得 ……14分
……14分
∵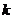 ,
,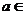
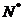 ,∴
,∴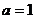 时,
时,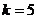 或
或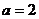 时,
时,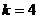 .
……15分
.
……15分
16. 方法一、证明:(Ⅰ)∵正方体
方法一、证明:(Ⅰ)∵正方体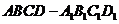 中,
中,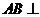 面
面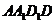 ,
,
又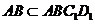 ∴平面
∴平面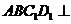 平面
平面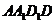 , ……4分
, ……4分
∵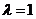 时,
时,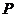 为
为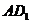 的中点,∴
的中点,∴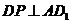 ,
,
又∵平面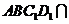 平面
平面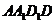
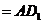 ,∴
,∴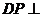 平面
平面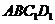 ,
,
又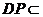 平面
平面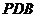 ,∴平面
,∴平面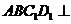 平面
平面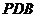 .………8分
.………8分
(Ⅱ)∵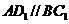 ,
, 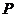 为线段
为线段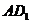 上的点,
上的点,
∴三角形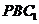 的面积为定值,即
的面积为定值,即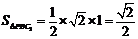 ………10分
………10分
又∵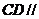 平面
平面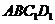 ,∴点
,∴点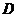 到平面
到平面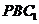 的距离为定值,即
的距离为定值,即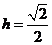 , ………12分
, ………12分
∴三棱锥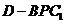 的体积为定值,即
的体积为定值,即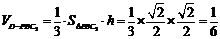 .
.
也即无论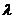 为何值,三棱锥
为何值,三棱锥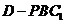 的体积恒为定值
的体积恒为定值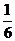 ;……………………14分
;……………………14分
15. 解法一:(I)由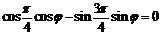 得
得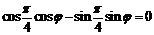
即 又
又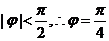
(Ⅱ)由(I)得, 依题意,
依题意, 又
又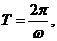 故
故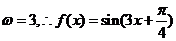
函数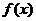 的图像向左平移
的图像向左平移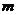 个单位后所对应的函数为
个单位后所对应的函数为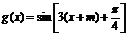
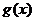 是偶函数当且仅当
是偶函数当且仅当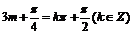 即
即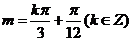 从而,最小正实数
从而,最小正实数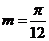
解法二:(I)同解法一
(Ⅱ)由(I)得, w.w.w.k.s.5.u.c.o.
w.w.w.k.s.5.u.c.o.  依题意,
依题意, 又
又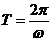 ,故
,故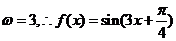
函数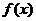 的图像向左平移
的图像向左平移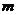 个单位后所对应的函数为
个单位后所对应的函数为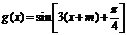
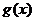 是偶函数当且仅当
是偶函数当且仅当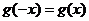 对
对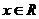 恒成立
恒成立
亦即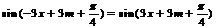 对
对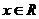 恒成立。
恒成立。
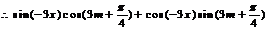

即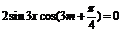 对
对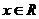 恒成立。
恒成立。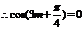
故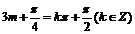
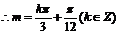 从而,最小正实数
从而,最小正实数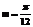
14. 解析 解析:由题意该函数的定义域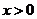 ,由
,由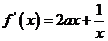 。因为存在垂直于
。因为存在垂直于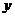 轴的切线,故此时斜率为
轴的切线,故此时斜率为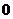 ,问题转化为
,问题转化为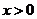 范围内导函数
范围内导函数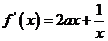 存在零点。
存在零点。
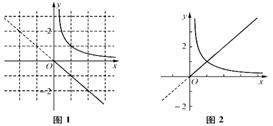
解法1 (图像法)再将之转化为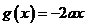 与
与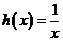 存在交点。当
存在交点。当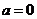 不符合题意,当
不符合题意,当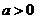 时,如图1,数形结合可得显然没有交点,当
时,如图1,数形结合可得显然没有交点,当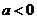 如图2,此时正好有一个交点,故有
如图2,此时正好有一个交点,故有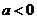 应填
应填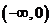 或是
或是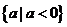 。
。
解法2 (分离变量法)上述也可等价于方程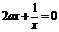 在
在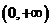 内有解,显然可得
内有解,显然可得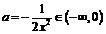
13.
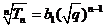
12. [解析]设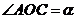
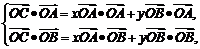 ,即
,即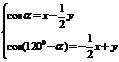
∴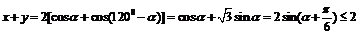
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com