
18. (本小题主要考查概率、解方程与解不等式等知识,考查数形结合、化归与转化的数学思想方法,以及运算求解能力)
(1)解:直线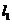 的斜率
的斜率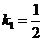 ,直线
,直线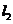 的斜率
的斜率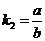 .
.
设事件 为“直线
为“直线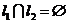 ”.
”.
 ,
,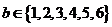 的总事件数为
的总事件数为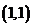 ,
,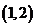 ,…,
,…,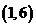 ,
,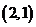 ,
,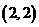 ,…,
,…,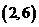 ,…,
,…,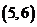 ,
,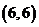 共36种.
共36种.
若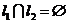 ,则
,则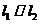 ,即
,即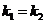 ,即
,即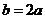 .
.
满足条件的实数对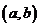 有
有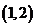 、
、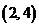 、
、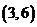 共三种情形.
共三种情形.
所以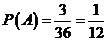 .
.
答:直线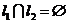 的概率为
的概率为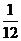 .
.
(2)解:设事件 为“直线
为“直线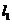 与
与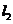 的交点位于第一象限”,由于直线
的交点位于第一象限”,由于直线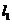 与
与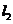 有交点,则
有交点,则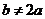 .
.
联立方程组 解得
解得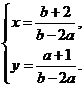
因为直线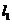 与
与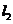 的交点位于第一象限,则
的交点位于第一象限,则
即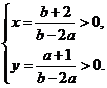 解得
解得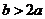 .
.
 ,
,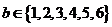 的总事件数为
的总事件数为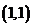 ,
,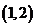 ,…,
,…,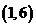 ,
,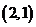 ,
,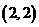 ,…,
,…,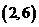 ,…,
,…,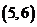 ,
,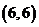 共36种.
共36种.
满足条件的实数对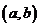 有
有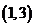 、
、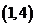 、
、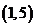 、
、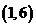 、
、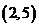 、
、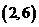 共六种.
共六种.
所以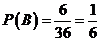 .
.
答:直线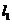 与
与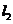 的交点位于第一象限的概率为
的交点位于第一象限的概率为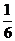 .
.
17.(本题满分15分)解:(1)由点P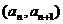 在直线
在直线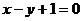 上,
上,
即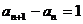 ,-----------------------------------------------2分
,-----------------------------------------------2分
且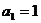 ,数列{
,数列{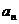 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列
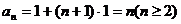 ,
,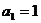 同样满足,所以
同样满足,所以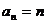 ---------------7分
---------------7分
(2)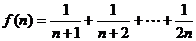
 ---------------------12分
---------------------12分

所以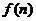 是单调递增,故
是单调递增,故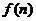 的最小值是
的最小值是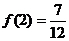 ----------------------15分
----------------------15分
16.(本题满分14分)
解:(Ⅰ)证明:连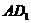
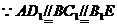
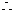 四边形
四边形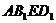 是平行四边形 ……2分
是平行四边形 ……2分
则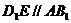
又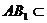 平面
平面 ,
,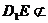 平面
平面
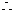
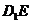 //平面
//平面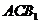 ……5分
……5分
(Ⅱ) 由已知得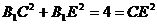 则
则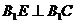 ……6分
……6分
由长方体的特征可知: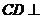 平面
平面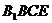 而
而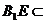 平面
平面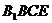 , 则
, 则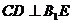 ……9分
……9分
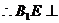 平面
平面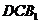 又
又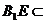 平面
平面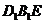
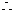 平面
平面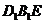
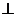 平面
平面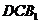 ………10分
………10分
(Ⅲ)四面体D1B1AC的体积
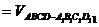
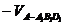
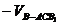
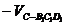
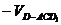
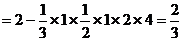 ………14分
………14分
8.  9.
36种 10. 4条 11. 9 12.
9.
36种 10. 4条 11. 9 12. 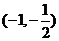 13
13 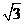 14. 1个
14. 1个
15解析:(解:(1)由向量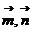 共线有:
共线有: 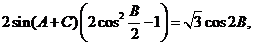
即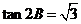 ,
4分
,
4分
又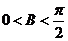 ,所以
,所以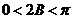 ,则
,则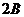 =
=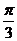 ,即
,即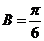 7分
7分
(2)由余弦定理得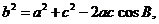
则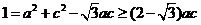 ,
,
所以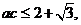 当且仅当
当且仅当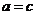 时等号成立 12分
时等号成立 12分
 所以
所以 .
14分
.
14分
1. 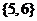 2.
2. 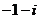 3. 4 4.
3. 4 4. 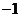 5.
5.  6.
6. 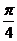 7.
7. 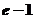
20.(本题满分16分)已知函数 在
在 上是减函数,在
上是减函数,在 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.
(1)求 的值;
的值;
(2)求 的取值范围;
的取值范围;
(3)试探究直线 与函数
与函数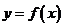 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.
数学试卷 第4页(共4页)
19. (本题满分16分)已知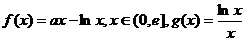 ,其中
,其中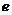 是自然常数,
是自然常数,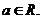
(1)讨论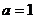 时,
时,  的单调性、极值;
的单调性、极值;
(2)求证:在(1)的条件下, ;
;
(3)是否存在实数 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
18. (本题满分15分)
已知直线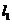 :
: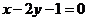 ,直线
,直线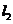 :
: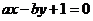 ,其中
,其中 ,
,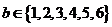 .
.
(1)求直线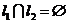 的概率;
的概率;
(2)求直线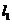 与
与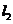 的交点位于第一象限的概率.
的交点位于第一象限的概率.
17. (本题满分15分)
已知数列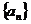 中,
中,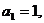 且点
且点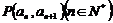 在直线
在直线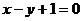 上.
上.
(1)求数列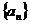 的通项公式;
的通项公式;
(2)若函数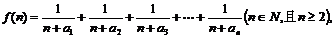 求函数
求函数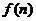 的最小值;
的最小值;
数学试卷 第3页(共4页)
16. (本题满分14分)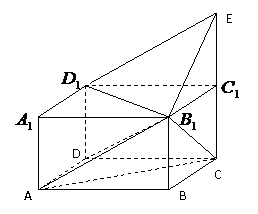
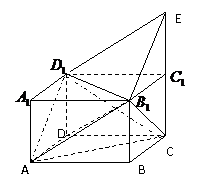
如图,在长方体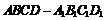 中,点
中,点 在棱
在棱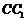 的延长线上,且
的延长线上,且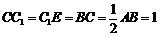 .
.
(Ⅰ)求证: ∥平面
∥平面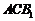 ;
;
(Ⅱ)求证:平面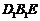
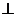 平面
平面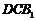 ;
;
(Ⅲ)求四面体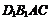 的体积.
的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com