
19.已知函数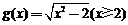 的导数为
的导数为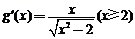 . 记函数
. 记函数
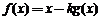
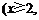 k为常数).
k为常数).
(1)若函数f(x)在区间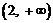 上为减函数,求
上为减函数,求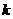 的取值范围;
的取值范围;
(2)求函数f(x)的值域.。
18.已知椭圆 的左右焦点分别为
的左右焦点分别为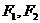 ,短轴两个端点为
,短轴两个端点为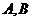 ,且四边形
,且四边形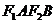 是边长为2的正方形。
是边长为2的正方形。
(1)求椭圆方程;
(2)若 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点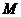 满足
满足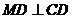 ,连接
,连接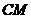 ,交椭圆于点
,交椭圆于点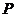 .证明:
.证明: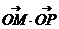 为定值;
为定值;
(3)在(2)的条件下,试问 轴上是否存在异于点
轴上是否存在异于点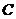 的定点
的定点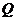 ,使得以
,使得以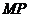 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点
的交点,若存在,求出点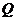 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
17.从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组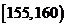 、第二组
、第二组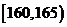 ;…第八组
;…第八组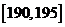 ,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为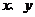 ,求满足
,求满足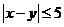 的事件概率.
的事件概率.
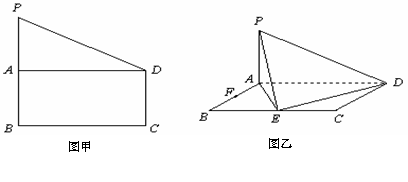
16.如图甲,在直角梯形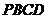 中,
中,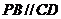 ,
,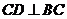 ,
,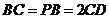 ,
,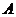 是
是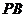 的中点. 现沿
的中点. 现沿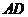 把平面
把平面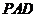 折起,使得
折起,使得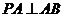 (如图乙所示),
(如图乙所示),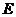 、
、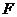 分别为
分别为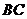 、
、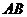 边的中点.
边的中点.
(Ⅰ)求证: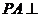 平面
平面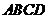 ;
;
(Ⅱ)求证:平面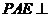 平面
平面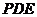 ;
;
(Ⅲ)在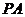 上找一点
上找一点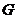 ,使得
,使得 平面
平面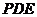 .
.
15.已知函数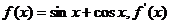 是
是 的导函数。
的导函数。
(1)求函数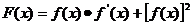 的最大值以及最小正周期;
的最大值以及最小正周期;
(2)若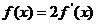 ,求
,求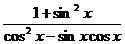 的值。
的值。
13.已知函数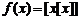 ,其中
,其中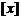 表示不超过x的最大整数,如:
表示不超过x的最大整数,如: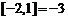 ,
,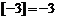 ,
, 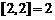 ,若
,若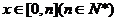 则
则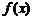 的值域中元素个数为
.
的值域中元素个数为
.
 14.如图,P是双曲线
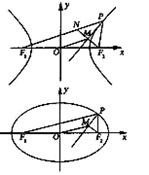
14.如图,P是双曲线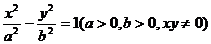 上的动点,F1、F2是双曲线的焦点,M是
上的动点,F1、F2是双曲线的焦点,M是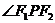 的平分线上一点,且
的平分线上一点,且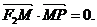 某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知
某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知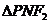 为等腰三角形,且M为F2M的中点,
为等腰三角形,且M为F2M的中点,
得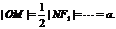 类似地:P是椭圆
类似地:P是椭圆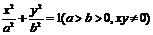
上的动点,F1、F2是椭圆的焦点,M是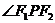 的平分线上一点,
的平分线上一点,
且 。则|OM|的取值范围是
.
。则|OM|的取值范围是
.
12.直线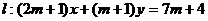 被以点
被以点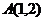 为圆心,3为半径的圆
为圆心,3为半径的圆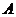 所截得的最短弦长为
。
所截得的最短弦长为
。
11.在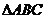 中,若
中,若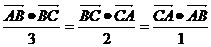 ,则
,则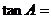 。
。
10.设函数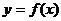 满足对一切的
满足对一切的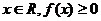 ,且
,且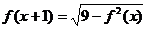 ,已知当
,已知当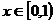 时,
时,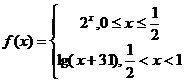 ,则
,则 。
。
9.在四面体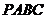 中,已知
中,已知 ,且各棱长的和为
,且各棱长的和为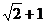 ,则这个四
,则这个四
面体体积的最大值是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com