
5.下列有关纯铁的描述正确的是
A.熔点比生铁的低
B.与相同浓度的盐酸反应生成氢气的速率比生铁的快
C.在潮湿空气中比生铁容易被腐蚀
D.在冷的浓硫酸中可钝化
4.等体积、等物质的量浓度的硫酸、氢氧化钠溶液分别放在甲、乙两烧杯中,各加等质量的铝,生成氢气的体积比为5∶6,则甲、乙两烧杯中的反应情况可能分别是
A.甲、乙中都是铝过量 B.甲中铝过量、乙中碱过量
C.甲中酸过量、乙中铝过量 D.甲中酸过量、乙中碱过量
3.在烧杯中加入水和苯(密度:0.88 g/cm3)各50 mL。将一小粒金属钠(密度:0.97 g/cm3)投入烧杯中。观察到的现象可能是
A.钠在水层中反应并四处游动
B.钠停留在苯层中不发生反应
C.钠在苯的液面上反应并四处游动
D.钠在苯与水的界面处反应并可能作上、下跳动
2.在氯化铁、氯化铜和盐酸混合溶液中加入铁粉,待反应结束,所剩余的固体滤出后能被磁铁吸引,则反应后溶液中存在较多的阳离子是
A.Cu2+ B.Fe3+ C.Fe2+ D.H+
1.下列块状金属在常温时能全部溶于足量浓HNO3的是
A.Ag B. Au C.Al D.Fe
21.(本小题满分14分)
解:(Ⅰ)分别令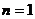 ,2,3,得
,2,3,得
∵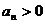 ,∴
,∴ ,
,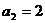 ,
, .………………………………………3分
.………………………………………3分
(Ⅱ)证法一:猜想: ,………………………………………………………4分
,………………………………………………………4分
由 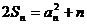 ①
①
可知,当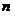 ≥2时,
≥2时, ②
②
①-②,得  ,即
,即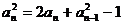 .………………6分
.………………6分
1)当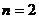 时,
时, ,∵
,∵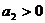 ,∴
,∴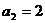 ;……………7分
;……………7分
2)假设当 (
( ≥2)时,
≥2)时, . 那么当
. 那么当 时,
时,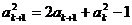
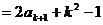
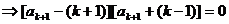 , ∵
, ∵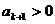 ,
, ≥2,∴
≥2,∴ ,
,
∴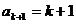 .
这就是说,当
.
这就是说,当 时也成立,
时也成立,
∴ (
(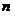 ≥2). 显然
≥2). 显然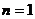 时,也适合.
时,也适合.
故对于n∈N*,均有 .…………………………………9分
.…………………………………9分
证法二:猜想: ,…………………………………………4分
,…………………………………………4分
1)当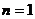 时,
时, 成立;……………………………………5分
成立;……………………………………5分
2)假设当 时,
时, .……………………………………6分
.……………………………………6分
那么当 时,
时,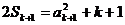 .∴
.∴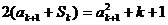 ,
,
∴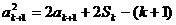
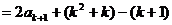
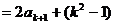
(以下同证法一)…………………………………………………………9分
(Ⅲ)证法一:要证 ≤
≤ ,
,
只要证 ≤
≤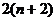 ,………………10分
,………………10分
即
 ≤
≤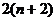 ,…………………11分
,…………………11分
将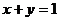 代入,得
代入,得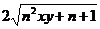 ≤
≤ ,
,
即要证 ≤
≤ ,即
,即 ≤1. …………………………12分
≤1. …………………………12分
∵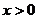 ,
, ,且
,且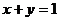 ,∴
,∴ ≤
≤ ,
,
即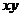 ≤
≤ ,故
,故 ≤1成立,所以原不等式成立. ………………………14分
≤1成立,所以原不等式成立. ………………………14分
证法二:∵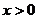 ,
, ,且
,且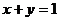 , ∴
, ∴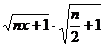 ≤
≤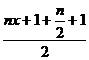 ①
①
当且仅当 时取“
时取“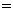 ”号. …………………………………11分
”号. …………………………………11分
∴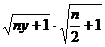 ≤
≤ ②
②
当且仅当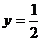 时取“
时取“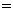 ”号. …………………………………12分
”号. …………………………………12分
①+②,得(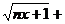
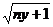 )
)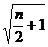 ≤
≤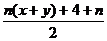
 ,
,
当且仅当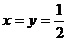 时取“
时取“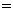 ”号. ……………………………………13分
”号. ……………………………………13分
∴ ≤
≤ .………………………………………14分
.………………………………………14分
证法三:可先证 ≤
≤ . ………………………………………10分
. ………………………………………10分
∵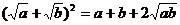 ,
,
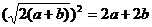 ,
, ≥
≥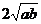 ,……………………………11分
,……………………………11分
∴ ≥
≥ ,
,
∴ ≥
≥ ,当且仅当
,当且仅当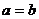 时取等号. ………………12分
时取等号. ………………12分
令 ,
,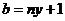 ,即得:
,即得: ≤
≤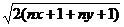
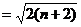 ,
,
当且仅当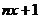
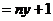 即
即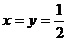 时取等号. ………………………14分
时取等号. ………………………14分
20.(本小题满分14分)
解:(1)当 时,由
时,由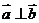 得
得 ,
,
 ;(
;( 且
且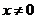 )
----------------------------------------------2分
)
----------------------------------------------2分
当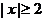 时,由
时,由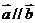 .得
.得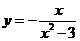 --------------------------------------4分
--------------------------------------4分
∴  ------------------------5分
------------------------5分
(2)当 且
且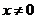 时,由
时,由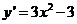 <0,解得
<0,解得 ,----------------6分
,----------------6分
当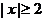 时,
时,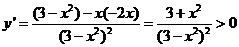 ------------------------------8分
------------------------------8分
∴函数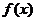 的单调减区间为(-1,0)和(0,1) -------------------------------9分
的单调减区间为(-1,0)和(0,1) -------------------------------9分
(3)对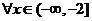
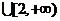 ,都有
,都有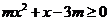 即
即 ,
,
也就是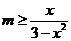 对
对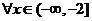
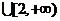 恒成立,----------------------------------11分
恒成立,----------------------------------11分
由(2)知当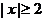 时,
时,
∴ 函数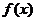 在
在 和
和 都单调递增---------------------------------------12分
都单调递增---------------------------------------12分
又 ,
,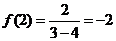
当 时
时 ,∴当
,∴当 时,
时,
同理可得,当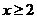 时,有
时,有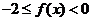 ,
,
综上所述得,对
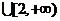 ,
, 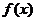 取得最大值2;
取得最大值2;
∴ 实数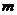 的取值范围为
的取值范围为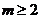 .----------------------------------------------------14分
.----------------------------------------------------14分
19.(本小题满分14分)
解:(1)当
 时,∵
时,∵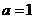 ,∴
,∴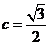 ,
,
 ∴
∴ ,
,
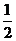 ,点
,点 ,
,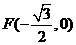 ,
,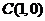 …………………… 2分
…………………… 2分
设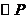 的方程为
的方程为 ,
,
由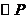 过点F,B,C得
过点F,B,C得
∴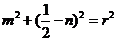 ①
①
 ②
② 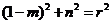 ③ ……………………
5分
③ ……………………
5分
由①②③联立解得: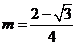 ,
,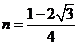 ,
, …………………… -7分
…………………… -7分
∴所求的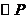 的方程为
的方程为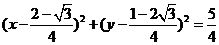 …………………… 8分
…………………… 8分
(2)∵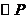 过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为
过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为 ④
…………………… 9分
④
…………………… 9分
∵BC的中点为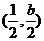 ,
,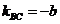
∴BC的垂直平分线方程为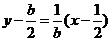 ⑤ ……………………
10分
⑤ ……………………
10分
由④⑤得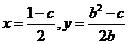 ,即
,即 …………………… 11分
…………………… 11分
∵ P 在直线
在直线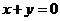 上,∴
上,∴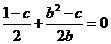
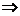
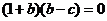
∵ 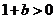 ∴
∴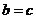 ,由
,由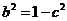 得
得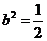 …………………… 13分
…………………… 13分
∴ 椭圆的方程为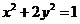 …………………… 14分
…………………… 14分
18. (本小题满分14分)
(本小题满分14分)
解:如图所示,
(Ⅰ)证明:因为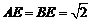 ,
,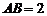 ,所以
,所以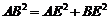 ,即
,即 ,…2分
,…2分
取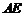 的中点
的中点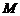 ,连结
,连结 ,则
,则 ,
,
又平面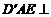 平面
平面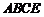 ,可得
,可得 平面
平面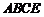 ,即得
,即得
 ,…………5分
,…………5分
从而 平面
平面 ,故
,故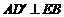 ……………………7分
……………………7分
(Ⅱ)如图建立空间直角坐标系,则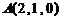 、
、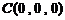 、
、 、
、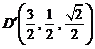 ,
, ,从而
,从而 ,
,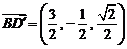 ,
, 。………9分
。………9分
设 为平面
为平面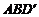 的法向量,
的法向量,
则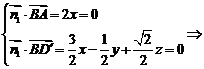 可以取
可以取 ……………………11分
……………………11分
设 为平面
为平面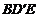 的法向量,
的法向量,
则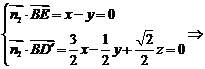 可以取
可以取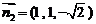 ……………………13分
……………………13分
因此, ,有
,有 ,即平面
,即平面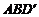
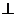 平面
平面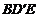 ,
,
故二面角 的大小为
的大小为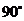 .……………………14分
.……………………14分
17.(本小题满分12分)
解:解:(1)不能被4整除的有两种情形;
①4个数均为奇数,概率为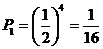 ………… 2分
………… 2分
②4个数中有3 个奇数,另一个为2,
概率为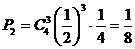 ………… 4分
………… 4分
故所求的概率为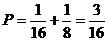 ………… 6分
………… 6分
(2) 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
4 |
|
P |
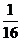 |
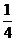 |
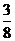 |
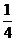 |
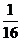 |
 服从二项分布
服从二项分布 ,则
,则 …………12分
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com