
5.有两排座位,前排4个座位,后排5个座位,现安排2人入座,并且这2人不相邻(一前一后也视为不相邻),那么不同坐法的种数为
A. 26 B. 29 C.49 D.58
4.向量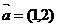 ,
, ,
,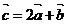 ,
,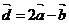 ,若
,若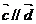 ,则实数
,则实数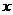 =
=
A.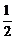 B.
B. C.
C.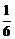 D.
D.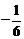
3.设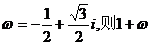 =
=
A.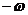 B.
B.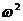 C.
C.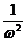 D.
D.

2.双曲线的方程为“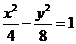 ”是“双曲线的离心率为
”是“双曲线的离心率为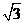 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
1. 设全集
设全集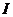 为R,
为R,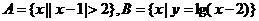 ,则下图1中阴影
,则下图1中阴影
部分表示的集合为
A. B.
B.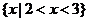 C.
C. D.
D. 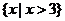
14.现有一批货物用轮船从上海洋山深水港运往青岛,已知该船航行的最大速度为35海里/小时,上海至青岛的航行距离约为500海里,每小时运输成本由燃料费用和其余费用组成.轮船每小时的燃料费用与轮船速度的平方成正比(比例系数为0.6),其余费用每小时960元.
(1)把全程运输y(元)表示为速度x(海里/小时)的函数;
(2)为了使全程运输成本最低,轮船应以多大速度行驶?
**15.数列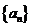 满足
满足
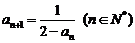 .
.
(1)证明:数列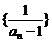 是等差数列;
是等差数列;
(2)求数列{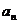 }的通项公式. 并证明数列{
}的通项公式. 并证明数列{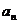 }是单调递增数列.
}是单调递增数列.
**16.设 、
、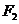 分别是椭圆
分别是椭圆 :
: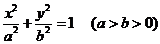 的左右焦点.
的左右焦点.
(1)设椭圆 上点
上点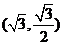 到两点
到两点 、
、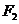 距离和等于
距离和等于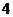 ,写出椭圆
,写出椭圆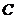 的方程和焦点坐标;
的方程和焦点坐标;
(2)设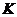 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段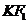 的中点
的中点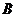 的轨迹方程.
的轨迹方程.
**17.已知函数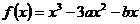 ,其中
,其中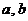 为实数.
为实数.
(1)若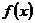 在
在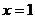 处取得的极值为
处取得的极值为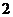 ,求
,求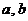 的值;
的值;
(2)若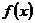 在区间
在区间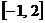 上为减函数,且
上为减函数,且 ,求
,求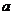 的取值范围.
的取值范围.
13.已知向量 ,
,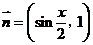
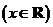 ,设函数
,设函数 .
.
(1)求函数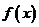 的值域;
的值域;
(2)已知锐角 的三个内角分别为
的三个内角分别为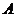 ,
,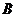 ,
,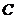 ,若
,若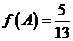 ,
,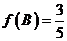 ,求
,求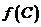 的值.
的值.
12.设函数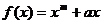 的导函数
的导函数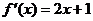 ,则数列
,则数列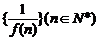 的前n项和是
.
的前n项和是
.
11.右图是一个几何体的三视图,根据图中数据,可得该几
何体的表面积是 .
10.已知|AB|=4,M是AB的中点,点P在平面内运动且保持|PA|+|PB|=6,则|PM|的最大值和最小值分别是 ( )
A.3和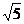 B.5和
B.5和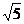 C.3和
C.3和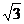 D.4和
D.4和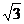
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com