
1. 动物细胞培养
(1)原理:细胞增殖
 (2)过程:
(2)过程:
(3)培养液的成分:液体培养基,包括无机盐、葡萄糖、维生素、氨基酸、动物血清
(4)动物细胞生长特点:贴壁生长和接触抑制
3.植物细胞工程的实际应用
植物繁殖的新途径:
① 植物体快速繁殖
② 作物脱毒:取植物分生区附近,如茎尖、根尖,因很少被病毒感染,甚至无病毒,而被用来培育无病毒植株。
③ 制作人工种子:利胚状体 + 人工种皮
④ 单倍体育种:大大缩短了育种年限。
2.基本技术:植物组织培养技术,植物体细杂交技术。
(1)植物组织培养技术
① 过程:
|

或细胞
|
|
脱分化:高度分化的植物器官、组织或细胞产生愈伤组织的过程
再分化:愈伤组织继续培养,重新分化成根或芽等器官的过程
愈伤组织:排列疏松、无规则,高度液泡化的无定型状态的薄壁细胞
② 培养基的成分:(半)固体培养基,主要是矿质元素、蔗糖、维生素、植物激素等。
③ 特点:
Ⅰ 外植体的选择:花和幼嫩的组织脱分化较为容易,而植物的茎、叶和成熟的老组织则较难。另外制备外植体时应选取有形成层的部分,因为形成层细胞易脱分化。
Ⅱ 严格的无菌条件:培养基上有细菌等微生物存在时,它们比植物细胞生长、繁殖得更快,而且它们会产生毒素,使培养的植物细胞很快中毒死亡。因此在培养过程中要求进行一系列的消毒、灭菌,并且要求无菌操作。
Ⅲ 完全的营养条件:离体的植物细胞失去了植物的自养能力,所以需要为其提供包括水、有机营养、矿质营养、维生素等营养物质。
Ⅳ 光照:离体的植物细胞、组织和器官脱分化形成愈伤组织时,需避光处理;而愈伤组织再分化形成植物幼苗时,需光照处理。
Ⅴ 激素调控:生长素含量高于细胞分裂素时,主要诱导植物组织脱分化和根原基的形成;当细胞分裂素的效应高于生长素时,主要诱导植物组织再分化和芽原基的形成。
④ 地位:是培育转基因植物、植物体细胞杂交培育植物新品种的最后一道工序。
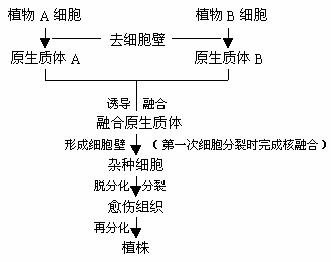 (2) 植物体细胞杂交技术
(2) 植物体细胞杂交技术
① 原理:细胞膜的流动性、植物细胞的全能性
② 过程
关键环节:
A.用纤维素酶和果胶酶去除细胞壁,获得有活力的原生质体;
B.原生质体间的融合:
融合方法:物理法(离心、振动、电激)
化学法(聚乙二醇PEG)
③ 植物细胞杂交与传统细胞杂交比较:
|
|
传统杂交 |
细胞杂交 |
|
依据 |
杂种优势 |
细胞全能性、原生质体融合 |
|
过程 |
自然发生,在母体完成胚发育 |
人工诱导融合,需组织培养 |
|
本质 |
精、卵两种生殖细胞结合,完成遗传物质的重新组合 |
不同生物的体细胞融合,完成遗传物质的融合 |
|
优点 |
杂种第一代生长整齐、植株健壮、产量高、抗虫抗病能力强 |
克服远源杂交不亲和障碍,实现不同种间的杂交 |
|
缺点 |
存在生殖隔离;杂种第二代会出现生长不齐、产量下降等现象 |
很多理论、技术问题未解决,距离推广应用有一定差距 |
|
目的 |
获得杂种优势,提高产量 |
获得优良性状 |
|
应用范围 |
种内 |
种内、种间均可 |
1.原理:细胞全能性
全能性表达的难易程度:植物细胞>动物细胞(动物细胞只有细胞核具有全能性);受精卵>生殖细胞(配子、精子、卵细胞)>体细胞; 幼嫩的细胞>衰老的细胞。在体细胞中:分化程度低的>分化程度高的 ,细胞分裂能力强的>细胞分裂能力弱的。
22.(本题满分14分)函数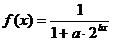 的定义域为R,且
的定义域为R,且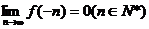
(1)求证:a>0,b<0;
(2)若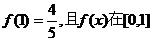 上的最小值为
上的最小值为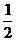 ,试求f(x)的解析式;
,试求f(x)的解析式;
(3)在(2)的条件下记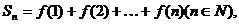 试比较
试比较
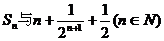 的大小并证明你的结论。
的大小并证明你的结论。
21. (本题满分12分)设双曲线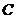 的中心在原点,以抛物线
的中心在原点,以抛物线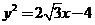 的顶点为双曲线的右焦点,抛物线的准线为双曲线的右准线。
的顶点为双曲线的右焦点,抛物线的准线为双曲线的右准线。
(1)
试求双曲线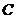 的方程;
的方程;
(2)
设直线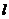 :
: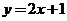 与双曲线
与双曲线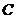 交于A、B两点,求|AB|;
交于A、B两点,求|AB|;
(3)
对于直线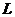 :
: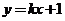 ,是否存在这样的实数k,使直线
,是否存在这样的实数k,使直线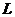 与双曲线
与双曲线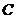 的交点A、B关于直线
的交点A、B关于直线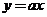 (
(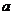 为常数)对称,若存在,求出
为常数)对称,若存在,求出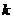 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
20. (本题满分12分)(理)已知点的序列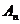 (
(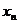 ,0),
,0),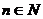 ,其中
,其中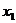 =0,
=0,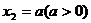 ,A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段
,A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段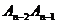 的中点,…。
的中点,…。
(I)写出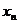 与
与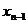 、
、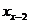 之间的关系式(
之间的关系式(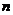 ≥3);
≥3);
(II)设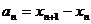 ,计算
,计算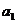 ,
,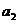 ,
,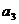 ,由此推测数列{
,由此推测数列{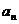 }的通项公式,并加以证明;
}的通项公式,并加以证明;
(III)求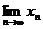 。
。
(文)已知数列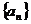 是等差数列,且
是等差数列,且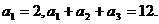
(Ⅰ)求数列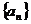 的通项公式;
的通项公式;
(Ⅱ)令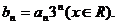 求数列
求数列 前n项和的公式。
前n项和的公式。
19.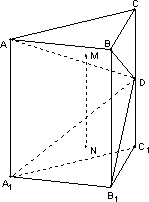 (本小题满分12分)如图,直三棱柱ABC-A1B1C1中,
(本小题满分12分)如图,直三棱柱ABC-A1B1C1中,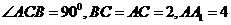 ,D为棱CC1上的一动点,M、N分别为
,D为棱CC1上的一动点,M、N分别为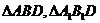 的重心.
的重心.
(1)求证: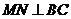 ;
;
(2)若二面角C-AB-D的大小为 ,求点C1到平面A1B1D的距离;
,求点C1到平面A1B1D的距离;
(3)若点C在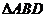 上的射影正好为M,试判断点C1在
上的射影正好为M,试判断点C1在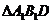 的射影是否为N?并说明理由.
的射影是否为N?并说明理由.
18.(本题满分12分) (理)摇奖器有10个小球,其中8个小球上标有数字2,2个小球上标有数字5,现摇出3个小球,规定所得奖金(元)为这3个小球上记号之和,求此次摇奖获得奖金数额的数学期望.
(文)某学生语、数、英三科考试成绩,在一次考试中排名全班第一的概率:语文为0.9,数学为0.8,英语为0.85,问一次考试中
(Ⅰ)三科成绩均未获得第一名的概率是多少?
(Ⅱ)恰有一科成绩未获得第一名的概率是多少?
.
17.(本题满分12分)已知函数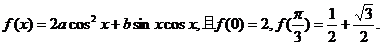
(1)求f(x)的最大值与最小值;
(2)若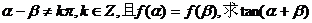 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com